题目内容
7．
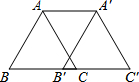如图，将边长为4个单位的等边△ABC沿边BC向右平移3个单位得到△A′B′C′，则四边形AA′C′B的周长为18．
分析 先根据平移的性质，求出AA′及CC′的值，然后由边长为4个单位的等边△ABC，可得：AB=BC=A′C′=4，然后根据四边形的周长公式即可求出四边形AA′C′B的周长．
解答 解：∵将边长为4个单位的等边△ABC沿边BC向右平移3个单位得到△A′B′C′，
∴AA′=CC′=3，AB=BC=A′C′=4，
∴四边形AA′C′B的周长=AB+AA′+A′C′+CC′+BC=4+3+4+3+4=18．
故答案为：18．
点评 此题考查了平移的性质，解题的关键是：熟记平移的性质：平移不改变图形的大小与形状，对应点之间的距离即是平移的距离．
练习册系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
17．
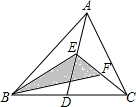如图，在△ABC中，已知点D、E、F分别是边BC、AD、CE上的中点，且S△ABC=4，则S△BFF=（ ）
如图，在△ABC中，已知点D、E、F分别是边BC、AD、CE上的中点，且S△ABC=4，则S△BFF=（ ）| A． | 2cm2 | B． | 1cm2 | C． | 0.5cm2 | D． | 0.25 cm2 |
15．
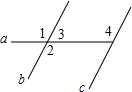如图，在所标记的角中，同位角是（ ）
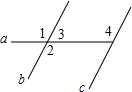如图，在所标记的角中，同位角是（ ）| A． | ∠1和∠2 | B． | ∠1和∠4 | C． | ∠1和∠3 | D． | ∠2和∠3 |
12．在Rt△ABC中，∠ACB=90°，AC=CB，CD是斜边AB的中线，若AB=2$\sqrt{2}$，则点D到BC的距离为（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | $\frac{\sqrt{2}}{2}$ |
19．不能判定四边形ABCD为平行四边形的题设是（ ）
| A． | AB=CD，AD∥BC | B． | AB$\stackrel{∥}{=}$CD | C． | AB=CD，AD=BC | D． | AB∥CD，AD∥BC |
