题目内容

16．先化简，再求值：（1-$\frac{2}{a}$）÷（a-$\frac{4a-4}{a}$），其中a=$\sqrt{2-m}+\sqrt{2m-4}$+$\sqrt{5}$．

分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，根据负数没有平方根求出m的值，进而确定出a的值，代入计算即可求出值．

解答 解：原式=$\frac{a-2}{a}$÷$\frac{{a}^{2}-4a+4}{a}$=$\frac{a-2}{a}$•$\frac{a}{（a-2）^{2}}$=$\frac{1}{a-2}$，
∵a=$\sqrt{2-m}$+$\sqrt{2m-4}$+$\sqrt{5}$，
∴$\left\{\begin{array}{l}{2-m≥0}\\{2m-4≥0}\end{array}\right.$，即m=2，a=$\sqrt{5}$，
则原式=$\frac{1}{\sqrt{5}-2}$=$\sqrt{5}$+2．

点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
6．等腰直角三角形的直角边为2，则斜边的长为（　　）
A．$\sqrt{2}$B．2$\sqrt{2}$C．1D．2
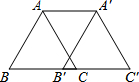7．如图，将边长为4个单位的等边△ABC沿边BC向右平移3个单位得到△A′B′C′，则四边形AA′C′B的周长为18．
4．（1）如图1，两个等边三角形ABC和A1B1C1的中心（点O）相同，且满足AB∥A1B1，BC∥B1C1，AC∥A1C1，可知AB与 A1B1，BC与B1C1，AC与A1C1之间的距离相等，直线MQ分别交三角形相邻两边于点M、N、P、Q，与AB所成夹角为∠α
①当∠α=30°时，求$\frac{MN}{PQ}$的值；
②当30°＜∠α＜90°，请用含∠α的式子表示$\frac{MN}{PQ}$；
（2）如图2，两个正方形ABCD和A1B1C1D1的中心（点O）相同，且满足AB∥A1B1，BC∥B1C1，CD∥C1D1，AD∥A1D1，可知AB与A1B1，BC与B1C1，CD与C1D1，AD与A1D1之间的距离相等，直线MQ分别交正方形相邻两边于点M、N、P、Q，与AB所成夹角为∠α
①当∠α=30°时，求$\frac{MN}{PQ}$的值；
②当0°＜∠α＜90°，请用含∠α的式子表示$\frac{MN}{PQ}$；
（3）根据（1）、（2）的研究，如果正n边形（n＞4）的位置关系也满足同样的条件（如图3），正n边形相邻两边被直线MQ截得的两条线段为MN，PQ，请用含n，∠α（0°＜∠α＜90°）的式子表示$\frac{MN}{PQ}$．
11．在平面直角坐标系中，如图①，将线段AB平移至线段CD，连接AC、BD．
（1）直接写出图中相等的线段、平行的线段．
（2）已知A（-3，0）、B（-2，-2），点C在y轴的正半轴上，点D在第一象限内，且S△ACO=5，求点C、D的坐标．
（3）如图②，在平面直角坐标系中，已知一定点M（1，0），两个动点E（a，2a+1）、F（b，-2b+3），请你探索是否存在以两个动点E、F为端点的线段EF平行于线段OM且等于线段OM？若存在，求以点O、M、E、F为顶点的四边形的面积；若不存在，请说明理由．
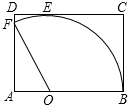1．如图，从矩形ABCD中剪出一个圆心角为120°的扇形OBF，扇形OBF与CD相切，切点为E，用这个扇形围成一个圆锥．若矩形ABCD的面积为54，则围成的圆锥的高为4$\sqrt{2}$．
8．抛物线y=mx2+（m-3）x-3（m＞0）与x轴交于A，B两点，且点A在点B的左侧，与y轴交于点C．
（1）当OB=OC时，求此时抛物线函数解析式；
（2）当△ABC为等腰三角形时，求m的值；
（3）若点P（x1，b）与点Q（x2，b）在（1）中抛物线上，且x1＜x2，PQ=n，求4x12-2x2n+6n+3的值．
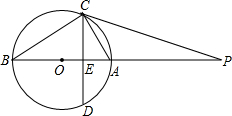5．如图，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB，垂足为E，且PC2=PE•PO
（1）求证：PC是⊙O的切线．
（2）若OE：EA=1：2，PA=6，求⊙O的半径．
（3）求sin∠PCA的值．
6．在一个圆柱形水池内，有一个进水管和一个出水管，进水管流水速度是出水管流水速度的两倍．开始时有一满池水，出水管开始放水，到池水只有一半池时，打开进水管放水（此时出水管不关）直到放满池水关闭进水管，再由出水管放完池水．则在这一过程水池中的水量V随时间t的变化关系的图象是（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网