题目内容
2.计算:(1)$\sqrt{2}$×3$\sqrt{2}$
(2)($\frac{1}{6}$)-1-20090+|-2$\sqrt{5}$|-$\sqrt{20}$
(3)$\sqrt{24}+\sqrt{12}$-($\sqrt{6}-\sqrt{27}$)
(4)$\frac{3}{\sqrt{3}}-(\sqrt{3})^{2}$+(π+$\sqrt{3}$)0-$\sqrt{27}$+|$\sqrt{3}$-2|
分析 (1)根据二次根式的乘法法则运算;
(2)根据零指数幂和负整数指数幂得到原式=6-1+2$\sqrt{5}$-2$\sqrt{5}$,然后合并即可;
(3)先把各二次根式化为最简二次根式,然后去括号合并即可;
(4)根据二次根式的性质和零指数幂的意义得到原式=$\sqrt{3}$-3+1-3$\sqrt{3}$+2-$\sqrt{3}$,然后合并即可.
解答 解:(1)原式=3×2
=6;
(2)原式=6-1+2$\sqrt{5}$-2$\sqrt{5}$
=5;
(3)原式=2$\sqrt{6}$+2$\sqrt{3}$-$\sqrt{6}$+3$\sqrt{3}$
=$\sqrt{6}$+5$\sqrt{3}$;
(4)原式=$\sqrt{3}$-3+1-3$\sqrt{3}$+2-$\sqrt{3}$
=-3$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和负整数指数幂.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
13.△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列命题是假命题的是( )
| A. | 若∠C-∠B=∠A,则△ABC是直角三角形 | |
| B. | 若c2=b2-a2,则△ABC是直角三角形且∠C是直角 | |
| C. | 若(c+a)(c-a)=b2,则△ABC是直角三角形 | |
| D. | 若∠A:∠B:∠C=5:2:3,则△ABC是直角三角形且∠A为直角 |
14.计算(a2)4÷a5÷a的结果为( )
| A. | a5 | B. | a4 | C. | a3 | D. | a2 |
12.已知关于x的方程2x+a-9=0的解是x=2,则a的值为( )
| A. | -7 | B. | 7 | C. | -5 | D. | 5 |
 如图,AB∥CD,EF分别交AB、CD于点F、E,FG平分∠EFC,交AB于G;若∠1=80°,求∠FGE的度数.
如图,AB∥CD,EF分别交AB、CD于点F、E,FG平分∠EFC,交AB于G;若∠1=80°,求∠FGE的度数.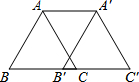 如图,将边长为4个单位的等边△ABC沿边BC向右平移3个单位得到△A′B′C′,则四边形AA′C′B的周长为18.
如图,将边长为4个单位的等边△ABC沿边BC向右平移3个单位得到△A′B′C′,则四边形AA′C′B的周长为18.