题目内容
15．
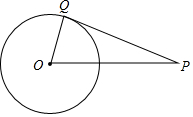如图，点Q在⊙O上，分别根据下列条件，判定直线PQ与⊙O是否相切（1）OQ=6，OP=10，PQ=8
（2）∠O=67.3°，∠P=22°42′．
分析 （1）根据勾股定理的逆定理得到OQ⊥PQ，
于是得到直线PQ与⊙O相切；
（2）根据三角形的内角和得到∠Q=180°-∠O-∠P=90°，于是得到结论．
解答 解：（1）∵OQ2+PQ2=62+82=102=OP2，
∴∠Q=90°，
∴OQ⊥PQ，
∵点Q在⊙O上，
∴直线PQ与⊙O相切；
（2）∵∠O=67.3°，∠P=22°42′，
∴∠Q=180°-∠O-∠P=90°，
∴OQ⊥PQ，
∵点Q在⊙O上，
∴直线PQ与⊙O相切．
点评 本题考查了切线的判定，勾股定理的逆定理，度、分、秒的换算，熟练掌握切线的判定定理是解题的关键．
练习册系列答案
相关题目
5．若直线y=mx+6（m≠0）与双曲线y=$\frac{n}{x}$（n≠0）在第一象限有公共点，则（ ）
| A． | mn＞-9 | B． | -9≤mn≤0 | C． | -4≤mn≤0 | D． | mn≥-9且mn≠0 |
如图．在△ABC中．已知CD是AB上的高，且CD=$\frac{1}{2}$AB．E，F分别是AC，BC的中点，求证：以EF为直径的⊙O与AB相切．
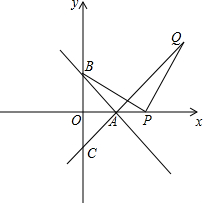直线y=-x+2与X轴、y轴交于A、B两点，C在y轴的负半轴上，且OC=OB．
已知：如图，在正方形ABCD外取一点E，连接AE，BE，DE．过点A作AE的垂线AP交DE于点P．若AE=AP=1，PB=$\sqrt{6}$，下列结论：