题目内容
16.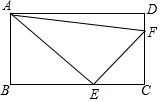 如图,在矩形ABCD中,AB=2,BC=3,AE是∠BAD的平分线,EF⊥AE,则AF的长为( )
如图,在矩形ABCD中,AB=2,BC=3,AE是∠BAD的平分线,EF⊥AE,则AF的长为( )| A. | 3$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | $\sqrt{10}$ |
分析 由于四边形ABCD是矩形,得到CD=AB=2,AD=BC=3,∠B=∠C=∠D=∠BAD=90°,根据AE是∠BAD的平分线,得到∠BAE=45°,推出△ABE是等腰直角三角形,求得CE=1,根据已知条件得到△EFC是等腰直角三角形,求得DF=1,根据勾股定理即可得到结论.
解答 解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠B=∠C=∠D=∠BAD=90°,
∵AE是∠BAD的平分线,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴BE=AB=2,
∴CE=1,
∵EF⊥AE,
∴∠AEF=90°,
∴∠FEC=45°,
∴△EFC是等腰直角三角形,
∴CF=CE=1,
∴DF=1,
∴AF=$\sqrt{D{F}^{2}+A{D}^{2}}$=$\sqrt{10}$,
故选D.
点评 本题考查了矩形的性质,等腰直角三角形的判定和性质,勾股定理,角平分线的定义,熟练掌握矩形的性质是解题的关键.

练习册系列答案
相关题目
11.将抛物线y=ax2+bx+c向右平移2个单位长度,再向下平移3个单位长度后,所得抛物线解析式为y=x2+2x-3,则a,b,c的值为( )
| A. | a=1,b=6,c=8 | B. | a=1,b=-2,c=3 | C. | a=1,b=4,c=-6 | D. | a=1,b=0,c=-6 |
 如图.在△ABC中.已知CD是AB上的高,且CD=$\frac{1}{2}$AB.E,F分别是AC,BC的中点,求证:以EF为直径的⊙O与AB相切.
如图.在△ABC中.已知CD是AB上的高,且CD=$\frac{1}{2}$AB.E,F分别是AC,BC的中点,求证:以EF为直径的⊙O与AB相切. 如图,由观察可知,三角形的中心投影是一个三角形,它还可以是线段.
如图,由观察可知,三角形的中心投影是一个三角形,它还可以是线段. 已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线AP交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:
已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线AP交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论: 在矩形AOBC中,OB=4,OA=3,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系xOy,F是边BC上的一个动点(不与B,C重合),过点F的反比例函数y=$\frac{k}{x}$(k>0)的图象与边AC交于点E,连接OE,OF.
在矩形AOBC中,OB=4,OA=3,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系xOy,F是边BC上的一个动点(不与B,C重合),过点F的反比例函数y=$\frac{k}{x}$(k>0)的图象与边AC交于点E,连接OE,OF.