题目内容
12. 如图,已知矩形纸片的一条边经过直角三角形纸片的直角顶点,若矩形纸片的一组对边与直角三角形纸片的两条直角边相交成∠1、∠2,则∠2-∠1=90°.
如图,已知矩形纸片的一条边经过直角三角形纸片的直角顶点,若矩形纸片的一组对边与直角三角形纸片的两条直角边相交成∠1、∠2,则∠2-∠1=90°.
分析 先根据平角的定义得出∠3=180°-∠2,再由平行线的性质得出∠4=∠3,根据∠4+∠1=90°即可得出结论.
解答  解:∵∠2+∠3=180°,
解:∵∠2+∠3=180°,
∴∠3=180°-∠2.
∵直尺的两边互相平行,
∴∠4=∠3,
∴∠4=180°-∠2.
∵∠4+∠1=90°,
∴180°-∠2+∠1=90°,即∠2-∠1=90°.
故答案为:90°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
20.先化简:$\frac{{x}^{2}+x}{{x}^{2}-2x+1}$÷($\frac{2}{x-1}$-$\frac{1}{x}$),再从-2<x<3的范围内选取一个你最喜欢的值代入,求值.
4. 如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )
 如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )| A. | 80° | B. | 100° | C. | 60° | D. | 40° |
1. 如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则$\frac{DE}{EF}$的值为( )
如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则$\frac{DE}{EF}$的值为( )
 如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则$\frac{DE}{EF}$的值为( )
如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则$\frac{DE}{EF}$的值为( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
 如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.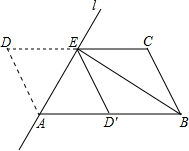 如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.
如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.