题目内容
4．
如图，四边形ABCD内接于⊙O，已知∠ADC=140°，则∠AOC的大小是（ ）| A． | 80° | B． | 100° | C． | 60° | D． | 40° |
分析 根据圆内接四边形的性质求得∠ABC=40°，利用圆周角定理，得∠AOC=2∠B=80°．
解答 解：∵四边形ABCD是⊙O的内接四边形，
∴∠ABC+∠ADC=180°，
∴∠ABC=180°-140°=40°．
∴∠AOC=2∠ABC=80°．
故选A．
点评 此题主要考查了圆周角定理以及圆内接四边形的性质，得出∠B的度数是解题关键．
练习册系列答案
相关题目
如图，⊙E的圆心E（3，0），半径为5，⊙E与y轴相交于A、B两点（点A在点B的上方），与x轴的正半轴交于点C，直线l的解析式为y=$\frac{3}{4}$x+4，与x轴相交于点D，以点C为顶点的抛物线过点B．
15．
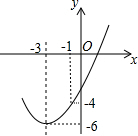如图，已知顶点为（-3，-6）的抛物线y=ax2+bx+c经过点（-1，-4），则下列结论中错误的是（ ）
如图，已知顶点为（-3，-6）的抛物线y=ax2+bx+c经过点（-1，-4），则下列结论中错误的是（ ）| A． | b2＞4ac | |
| B． | ax2+bx+c≥-6 | |
| C． | 若点（-2，m），（-5，n）在抛物线上，则m＞n | |
| D． | 关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1 |
如图，已知矩形纸片的一条边经过直角三角形纸片的直角顶点，若矩形纸片的一组对边与直角三角形纸片的两条直角边相交成∠1、∠2，则∠2-∠1=90°．
19．计算（-3）+（-9）的结果是（ ）
| A． | -12 | B． | -6 | C． | +6 | D． | 12 |
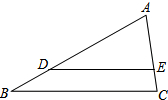如图，在△ABC中，点D、E分别在AB、AC边上，DE∥BC，若$\frac{AE}{AC}$=$\frac{3}{4}$，AD=6，则AB等于（ ）