题目内容
2. 如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.(1)求证:AB=CD.
(2)若AB=CF,∠B=30°,求∠D的度数.
分析 (1)易证得△ABE≌△CDF,即可得AB=CD;
(2)易证得△ABE≌△CDF,即可得AB=CD,又由AB=CF,∠B=30°,即可证得△ABE是等腰三角形,解答即可.
解答 证明:(1)∵AB∥CD,
∴∠B=∠C,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠C=∠B}\\{AE=DF}\end{array}\right.$,
∴△ABE≌△CDF(AAS),
∴AB=CD;
(2)∵△ABE≌△CDF,
∴AB=CD,BE=CF,
∵AB=CF,∠B=30°,
∴AB=BE,
∴△ABE是等腰三角形,
∴∠D=$\frac{1}{2}×(180°-30°)=75°$.
点评 此题考查全等三角形问题,关键是根据AAS证明三角形全等,再利用全等三角形的性质解答.

练习册系列答案
相关题目
17.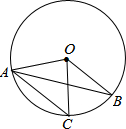 如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )
如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )
 如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )
如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )| A. | 25° | B. | 50° | C. | 60° | D. | 30° |
 如图,可以求出阴影部分的面积是a2-b2(写出两数平方差的形式)
如图,可以求出阴影部分的面积是a2-b2(写出两数平方差的形式)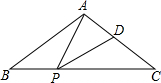 如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B. 如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=$\frac{3}{4}$x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=$\frac{3}{4}$x+4,与x轴相交于点D,以点C为顶点的抛物线过点B. 如图,已知矩形纸片的一条边经过直角三角形纸片的直角顶点,若矩形纸片的一组对边与直角三角形纸片的两条直角边相交成∠1、∠2,则∠2-∠1=90°.
如图,已知矩形纸片的一条边经过直角三角形纸片的直角顶点,若矩形纸片的一组对边与直角三角形纸片的两条直角边相交成∠1、∠2,则∠2-∠1=90°.