Question

17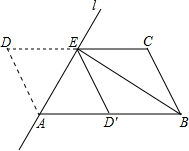．如图，将?ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，折痕l交CD边于点E，连接BE．
（1）求证：四边形BCED′是平行四边形；
（2）若BE平分∠ABC，求证：AB²=AE²+BE²．

Answer 1

分析 （1）利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA，进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形，进而求出四边形BCED′是平行四边形；
（2）利用平行线的性质结合勾股定理得出答案．

解答 证明：（1）∵将?ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，
∴∠DAE=∠D′AE，∠DEA=∠D′EA，∠D=∠AD′E，
∵DE∥AD′，
∴∠DEA=∠EAD′，
∴∠DAE=∠EAD′=∠DEA=∠D′EA，
∴∠DAD′=∠DED′，
∴四边形DAD′E是平行四边形，
∴DE=AD′，
∵四边形ABCD是平行四边形，
∴AB$\stackrel{∥}{=}$DC，
∴CE$\stackrel{∥}{=}$D′B，
∴四边形BCED′是平行四边形；

（2）∵BE平分∠ABC，
∴∠CBE=∠EBA，
∵AD∥BC，
∴∠DAB+∠CBA=180°，
∵∠DAE=∠BAE，
∴∠EAB+∠EBA=90°，
∴∠AEB=90°，
∴AB²=AE²+BE²．

点评 此题主要考查了平行四边形的判定与性质以及勾股定理等知识，得出四边形DAD′E是平行四边形是解题关键．