题目内容
8.已知关于x的一元二次方程kx2-3x-2=0有两个不相等的实数根.(1)求k的取值范围;
(2)若k为小于2的整数,且方程的根都是整数,求k的值.
分析 (1)根据一元二次方程kx2-3x-2=0有两个不相等的实数根得到△=9+8k>0且k≠0,求出k的取值范围;
(2)根据k的取值范围可知满足k的值有±1,然后把k值代入原方程验证满足题意k的值.
解答 解:(1)∵关于x的一元二次方程kx2-3x-2=0有两个不相等的实数根,
∴△>0且k≠0,
∴△=9+8k>0且k≠0,
∴$k>-\frac{9}{8}$且k≠0;
(2)∵k为小于2的整数,由(1)知道$k>-\frac{9}{8}$且k≠0,
∴k=-1,k=1,
∴当k=-1时,方程-x2-3x-2=0的根-1,-2都是整数,
当k=1时,方程x2-3x-2=0的根$\frac{{3±\sqrt{17}}}{2}$不是整数不符合题意,
综上所述,k=-1.
点评 本题主要考查了根的判别式的知识,解答本题的关键是根据根的判别式的意义求出k的取值范围,此题难度不大.

练习册系列答案
相关题目
20.计算:$\sqrt{32}-\sqrt{8}$的结果是( )
| A. | $\sqrt{24}$ | B. | $2\sqrt{6}$ | C. | $3\sqrt{2}$ | D. | $2\sqrt{2}$ |
6.已知:A(3,4),将OA绕原点O逆时针旋转90°得到OA′,则点A′的坐标是( )
| A. | (-3,4) | B. | (-4,3) | C. | (3,-4) | D. | (4,-3) |
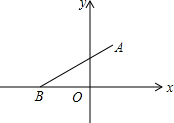 如图,在平面直角坐标系中,点A的坐标为(1,$\sqrt{3}$),点B在x轴的负半轴上,∠ABO=30°.
如图,在平面直角坐标系中,点A的坐标为(1,$\sqrt{3}$),点B在x轴的负半轴上,∠ABO=30°.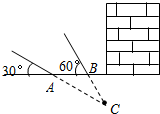 北京时间2015年04月25日14时11分,尼泊尔发生强烈地震,震级8.1级左右.在地震抢救中,某探测队探测出某建筑物下面有生命迹象,为了准确测出生命迹象所在的深度,他们在生命迹象上方建筑物的一侧地面上相距4米的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(参考数据:$\sqrt{3}$≈1.732,结果保留一位小数).
北京时间2015年04月25日14时11分,尼泊尔发生强烈地震,震级8.1级左右.在地震抢救中,某探测队探测出某建筑物下面有生命迹象,为了准确测出生命迹象所在的深度,他们在生命迹象上方建筑物的一侧地面上相距4米的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(参考数据:$\sqrt{3}$≈1.732,结果保留一位小数).