题目内容
13.已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.(1)①如图2,求出抛物线y=x2的“完美三角形”斜边AB的长;
②抛物线y=x2+1与y=x2的“完美三角形”的斜边长的数量关系是相等;
(2)若抛物线y=ax2+4的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线y=mx2+2x+n-5的“完美三角形”斜边长为n,且y=mx2+2x+n-5的最大值为-1,求m,n的值.
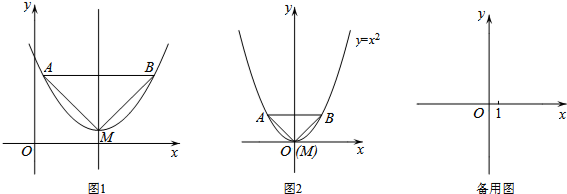
分析 (1)①①过点B作BN⊥x轴于N,根据△AMB为等腰直角三角形,AB∥x轴,所以∠BMN=∠ABM=45°,所以∠BMN=∠MBN,得到MN=BN,设B点坐标为(n,n),代入抛物线y=x2,得n=n2,解得n=1,n=0(舍去),所以B(1,1),求出BM的长度,利用勾股定理,即可解答;
②因为抛物线y=x2+1与y=x2的形状相同,所以抛物线y=x2+1与y=x2的“完美三角形”的斜边长的数量关系是相等;
(2)根据抛物线y=ax2与抛物线y=ax2+4的形状相同,所以抛物线y=ax2与抛物线y=ax2+4的“完美三角形”全等,所以抛物线y=ax2+4的“完美三角形”斜边的长为4,所以抛物线y=ax2的“完美三角形”斜边的长为4,从而确定B点坐标为(2,2)或(2,-2),把点B代入y=ax2中,得到$a=±\frac{1}{2}$.
(3))根据y=mx2+2x+n-5的最大值为-1,得到$\frac{{4m({n-5})-4}}{4m}=-1$,化简得mn-4m-1=0,抛物线y=mx2+2x+n-5的“完美三角形”斜边长为n,所以抛物线y=mx2的“完美三角形”斜边长为n,所以B点坐标为$({\frac{n}{2},-\frac{n}{2}})$,代入抛物线y=mx2,得${({\frac{n}{2}})^2}•m=-\frac{n}{2}$,mn=-2或n=0(不合题意舍去),所以$m=-\frac{3}{4}$,所以$n=\frac{8}{3}$.
解答 解:(1)①过点B作BN⊥x轴于N,如图2,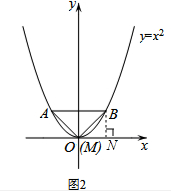
∵△AMB为等腰直角三角形,
∴∠ABM=45°,
∵AB∥x轴,
∴∠BMN=∠ABM=45°,
∴∠MBN=90°-45°=45°,
∴∠BMN=∠MBN,
∴MN=BN,
设B点坐标为(n,n),代入抛物线y=x2,
得n=n2,
∴n=1,n=0(舍去),
∴B(1,1)
∴MN=BN=1,
∴MB=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴MA=MB=$\sqrt{2}$,
在Rt△AMB中,AB=$\sqrt{M{B}^{2}+M{A}^{2}}$=2,
∴抛物线y=x2的“完美三角形”的斜边AB=2.
②∵抛物线y=x2+1与y=x2的形状相同,
∴抛物线y=x2+1与y=x2的“完美三角形”的斜边长的数量关系是相等;
故答案为:相等.
(2)∵抛物线y=ax2与抛物线y=ax2+4的形状相同,
∴抛物线y=ax2与抛物线y=ax2+4的“完美三角形”全等,
∵抛物线y=ax2+4的“完美三角形”斜边的长为4,
∴抛物线y=ax2的“完美三角形”斜边的长为4,
∴B点坐标为(2,2)或(2,-2),
把点B代入y=ax2中,
∴$a=±\frac{1}{2}$.
(3)∵y=mx2+2x+n-5的最大值为-1,
∴$\frac{{4m({n-5})-4}}{4m}=-1$,
∴mn-4m-1=0,
∵抛物线y=mx2+2x+n-5的“完美三角形”斜边长为n,
∴抛物线y=mx2的“完美三角形”斜边长为n,
∴B点坐标为$({\frac{n}{2},-\frac{n}{2}})$,
∴代入抛物线y=mx2,得${({\frac{n}{2}})^2}•m=-\frac{n}{2}$,
∴mn=-2或n=0(不合题意舍去),
∴$m=-\frac{3}{4}$,
∴$n=\frac{8}{3}$.
点评 本题考查了二次函数,解决本题的关键是理解“完美三角形”的定义,利用勾股定理,求出点B的坐标.

| A. | ±3 | B. | 3 | C. | -3 | D. | 9 |
| A. | x3+x3=2x6 | B. | (-x5)4=x20 | C. | xm•xn=xmn | D. | x8÷x2=x4 |
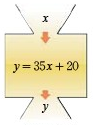 地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间的关系可以近似地用关系式y=35x+20来表示.当x的值是5时,y=195.
地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间的关系可以近似地用关系式y=35x+20来表示.当x的值是5时,y=195.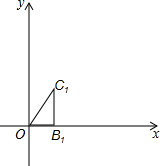 如图,在平面直角坐标系中,点B1(1,0),点C1(1,$\sqrt{3}$),将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB2=OC1,得到△OB2C1,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OB5C5,则△OB5C5中,点C5的坐标是(16,-16$\sqrt{3}$).
如图,在平面直角坐标系中,点B1(1,0),点C1(1,$\sqrt{3}$),将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB2=OC1,得到△OB2C1,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OB5C5,则△OB5C5中,点C5的坐标是(16,-16$\sqrt{3}$).