题目内容
6.已知:A(3,4),将OA绕原点O逆时针旋转90°得到OA′,则点A′的坐标是( )| A. | (-3,4) | B. | (-4,3) | C. | (3,-4) | D. | (4,-3) |
分析 作AB⊥x轴于B,A′C⊥x轴于C,先证明∠3=∠2,再证明△OCA′≌△ABO,得出OC=AB=4,A′C=OB=3,即可得出点A′的坐标.
解答 解:作AB⊥x轴于B,A′C⊥x轴于C,如图所示:
则∠ABO=∠OCA′=90°,
∴∠1+∠2=90°,
∵A(3,4),
∴OB=3,AB=4,
∵OA绕原点O逆时针旋转90°得到OA′,
∴∠AOA′=90°,OA′=OA,
∴∠1+∠3=90°,
∴∠3=∠2,
在△OCA′和△ABO中,$\left\{\begin{array}{l}{∠OCA′=∠ABO}&{\;}\\{∠3=∠2}&{\;}\\{OA′=OA}&{\;}\end{array}\right.$,
∴△OCA′≌△ABO(AAS),
∴OC=AB=4,A′C=OB=3,
∴点A′的坐标是(-4,3),
故选:B.
点评 本题考查了坐标与图形变化-旋转以及全等三角形的判定与性质;证明三角形全等是解决问题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
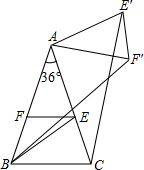 如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB.
如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB. 用圆规和直尺作图:已知∠α和线段a,求作△ABC,使∠A=∠α,AB=a,AC=2a.
用圆规和直尺作图:已知∠α和线段a,求作△ABC,使∠A=∠α,AB=a,AC=2a.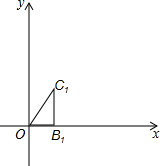 如图,在平面直角坐标系中,点B1(1,0),点C1(1,$\sqrt{3}$),将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB2=OC1,得到△OB2C1,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OB5C5,则△OB5C5中,点C5的坐标是(16,-16$\sqrt{3}$).
如图,在平面直角坐标系中,点B1(1,0),点C1(1,$\sqrt{3}$),将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB2=OC1,得到△OB2C1,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的2倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OB5C5,则△OB5C5中,点C5的坐标是(16,-16$\sqrt{3}$).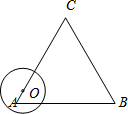 如图,动点O从边长为6的等边△ABC的顶点A出发,沿着A→C→B→A的路线匀速运动一周,速度为1个单位长度每秒.以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第三次相切时是点O出发后第( )秒.
如图,动点O从边长为6的等边△ABC的顶点A出发,沿着A→C→B→A的路线匀速运动一周,速度为1个单位长度每秒.以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第三次相切时是点O出发后第( )秒. 如图,AB∥CD,∠1=120°,∠ECD=70°,∠E的大小是50°.
如图,AB∥CD,∠1=120°,∠ECD=70°,∠E的大小是50°.