题目内容
17.反比例函数y=$\frac{{k}^{2}}{x}$(k为常数,k≠0)的图象位于第一、三象限.分析 首先判断比例系数的符号,然后根据其性质确定其图象所处的位置即可.
解答 解:∵k为常数,k≠0,
∴k2>0,
∴反比例函数y=$\frac{{k}^{2}}{x}$(k为常数,k≠0)的图象位于第一、三象限,
故答案为:一、三.
点评 本题主要考查了反比例函数y=$\frac{k}{x}$(k≠0)的性质:
①k>0时,函数图象在第一,三象限.在每个象限内y随x的增大而减小;
②k<0时,函数图象在第二,四象限.在每个象限内y随x的增大而增大.

练习册系列答案
相关题目
2.下列运算正确的是( )
| A. | x3+x3=2x6 | B. | (-x5)4=x20 | C. | xm•xn=xmn | D. | x8÷x2=x4 |




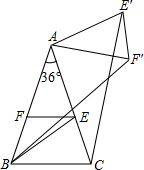 如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB.
如图,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转α角(0°<α<144°)得到△AE′F′,此时△AEF≌△AE′F′,∠FAF′=∠EAE′=α,连结CE′,BF′,当α=36°或72°时,CE′∥AB. 如图,AB∥CD,∠1=120°,∠ECD=70°,∠E的大小是50°.
如图,AB∥CD,∠1=120°,∠ECD=70°,∠E的大小是50°.