题目内容
10.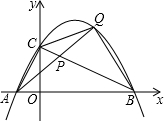 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.(1)①写出点A,B,C的坐标:A(-1,0),B(4,0),C(0,2);
②求证:△ABC是直角三角形;
(2)记△BCQ的面积为S,求S关于x的函数表达式;
(3)在点P的运动过程中,$\frac{PQ}{AP}$是否存在最大值?若存在,求出$\frac{PQ}{AP}$的最大值及点Q的坐标;若不存在,请说明理由.
分析 (1)①分别将x=0、y=0代入二次函数表达式中求出与之对应的y、x值,由此即可得出点C、A、B的坐标;
②由点A、B、C的坐标利用两点间的距离公式即可求出AB、AC、BC的长度,由AB2=25=AC2+BC2利用勾股定理的逆定理即可证出△ABC是直角三角形;
(2)连接OQ,设点Q的坐标为(x,-$\frac{1}{2}$x2+$\frac{3}{2}$x+2),根据三角形的面积公式结合S=S△OCQ+S△OBQ-S△OBC即可得出S=-x2+4x;
(3)过点Q作QH⊥BC于H,则△APC∽△QPH,根据相似三角形的性质可得出$\frac{PQ}{AP}=\frac{QH}{AC}=\frac{QH}{AC}$=$\frac{QH}{\sqrt{5}}$,再结合S△BCQ=$\frac{1}{2}$BC•QH=$\sqrt{5}$OH即可得出$\frac{PQ}{AP}$=$\frac{S}{5}$=-$\frac{1}{5}$(x-2)2+$\frac{4}{5}$,利用二次函数的性质即可解决最值问题.
解答 解:(1)①当x=0时,y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=2,
∴点C(0,2).
当y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=0时,有x2-3x-4=(x+1)(x-4)=0,
解得:x1=-1,x2=4,
∴A(-1,0),B(4,0).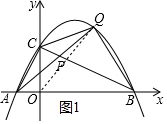
故答案为:-1,0;4,0;0,2.
②证明:∵A(-1,0),B(4,0),C(0,2),
∴AB=5,AC=$\sqrt{5}$,BC=2$\sqrt{5}$,
∴AB2=25=AC2+BC2,
∴△ABC是直角三角形.
(2)连接OQ,如图1所示.
设点Q的坐标为(x,-$\frac{1}{2}$x2+$\frac{3}{2}$x+2),
∴S=S△OCQ+S△OBQ-S△OBC=$\frac{1}{2}$×2•x+$\frac{1}{2}$×4•(-$\frac{1}{2}$x2+$\frac{3}{2}$x+2)-$\frac{1}{2}$×2×4=-x2+4x.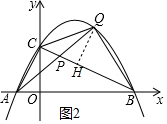
(3)过点Q作QH⊥BC于H,如图2所示.
∵∠ACP=∠QHP=90°,∠APC=∠QPH,
∴△APC∽△QPH,
∴$\frac{PQ}{AP}=\frac{QH}{AC}=\frac{QH}{AC}$=$\frac{QH}{\sqrt{5}}$.
∵S△BCQ=$\frac{1}{2}$BC•QH=$\sqrt{5}$OH,
∴QH=$\frac{S}{\sqrt{5}}$,
∴$\frac{PQ}{AP}$=$\frac{S}{5}$=$\frac{1}{5}$(-x2+4x)=-$\frac{1}{5}$(x-2)2+$\frac{4}{5}$,
∴当x=2时,$\frac{PQ}{AP}$取最大值,最大值为$\frac{4}{5}$,此时点Q的坐标为(2,3).
点评 本题考查了二次函数的综合应用、勾股定理的逆定理、两点间的距离公式、二次函数的性质、相似三角形的判定与性质以及三角形的面积,解题的关键是:(1)①分别将x=0、y=0代入二次函数表达式中求出与之对应的y、x值;②利用两点间的距离公式找出AB2=25=AC2+BC2;(2)利用分割图形求面积法找出S关于x的表达式;(3)利用相似三角形的性质结合(2)的结论找出$\frac{PQ}{AP}$=-$\frac{1}{5}$(x-2)2+$\frac{4}{5}$.

 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案| A. | $\frac{ab}{a+b}$小时 | B. | $\frac{a+b}{ab}$小时 | C. | a+b小时 | D. | $\frac{1}{a+b}$小时 |
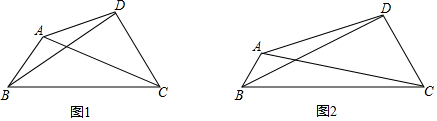
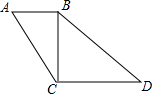 已知,如图,∠ABC=∠BCD=90°,AC=15,sinA=$\frac{4}{5}$,BD=20,求∠D的三个三角函数值.
已知,如图,∠ABC=∠BCD=90°,AC=15,sinA=$\frac{4}{5}$,BD=20,求∠D的三个三角函数值.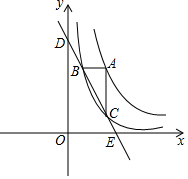 如图,点A在函数y=$\frac{4}{x}$(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=$\frac{1}{x}$图象于点B,C,直线BC与坐标轴的交点为D,E.
如图,点A在函数y=$\frac{4}{x}$(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=$\frac{1}{x}$图象于点B,C,直线BC与坐标轴的交点为D,E.