题目内容
20.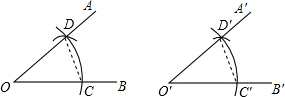 利用直尺和圆规作一个角等于已知角的作法如下:
利用直尺和圆规作一个角等于已知角的作法如下:①以点O为圆心,以任意长为半径画弧,分别交OA、OB于点D、C;
②作射线O′B′,以点O′为圆心,以OC或OD长为半径画弧,交O′B′于点C′;
③以点C′为圆心,以CD长为半径画弧,两弧交于点D′;
④过点D′作射线O′A′,∴∠A′O′B′为所求.
(1)请将上面的作法补充完整;
(2)△OCD≌△O′C′D′的依据是SSS.
分析 (1)直接利用基本作图方法进而填空得出答案;
(2)利用全等三角形的判定方法得出答案.
解答 解:(1)①以点O为圆心,以任意长为半径画弧,分别交OA、OB于点D、C;
②作射线O′B′,以点O′为圆心,以 OC或OD长为半径画弧,交O′B′于点C′;
③以点C′为圆心,以 CD长为半径画弧,两弧交于点D′;
④过点D′作射线O′A′,∴∠A′O′B′为所求.
故答案为:OC或OD;CD;
(2)由题意可得:在△OCD和△O′C′D′中
∵$\left\{\begin{array}{l}{OD=O′D′}\\{OC=O′C′}\\{DC=D′C′}\end{array}\right.$
∴△OCD≌△O′C′D′(SSS),
故△OCD≌△O′C′D′的依据是SSS.
故答案为:SSS.
点评 此题主要考查了基本作图以及全等三角形的判定,正确掌握基本作图方法是解题关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
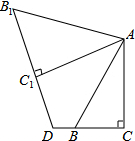 已知,如图,在△ABC中,∠C=90°,将△ABC绕点A按顺时针方向旋转得△AB1C1,延长B1C1交CB的延长线于D,求证:DC1-DB=B1C1.
已知,如图,在△ABC中,∠C=90°,将△ABC绕点A按顺时针方向旋转得△AB1C1,延长B1C1交CB的延长线于D,求证:DC1-DB=B1C1.