题目内容
城市规划期间,欲拆除一电线杆AB,已知距电线杆AB水平距离14m的D处有一大坝,背水坡CD的坡度i=1:2,坝高CF为2m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道.
(1)求BF的长;
(2)在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?请说明理由.
(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域)(
≈1.732,
≈1.414)

(1)求BF的长;
(2)在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?请说明理由.
(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域)(
| 3 |
| 2 |

考点:解直角三角形的应用-仰角俯角问题,解直角三角形的应用-坡度坡角问题
专题:
分析:(1)过C作CM⊥AB于M,那么AB的长度就是AM+MB也就是AM+CF.要求AM的长,需要知道CM的长,也就是BF的长;
(2)求需不需要将人行道封上实际上就是比较AB与BE的长短,已知BD,DF的长度,那么AB的长度也就求出来了,现在只需要知道BE的长度即可,有BF的长,ED的长,缺少的是DF的长,根据“背水坡CD的坡度i=1:2,坝高CF为2m”,DF是很容易求出的,这样有了AB的长,由了BE的长,就可以判断出是不是需要封上人行道了.
(2)求需不需要将人行道封上实际上就是比较AB与BE的长短,已知BD,DF的长度,那么AB的长度也就求出来了,现在只需要知道BE的长度即可,有BF的长,ED的长,缺少的是DF的长,根据“背水坡CD的坡度i=1:2,坝高CF为2m”,DF是很容易求出的,这样有了AB的长,由了BE的长,就可以判断出是不是需要封上人行道了.
解答:解:(1)如图,作CM⊥AB于点M,则MBFC为矩形.
∴BM=CF=2,BF=CM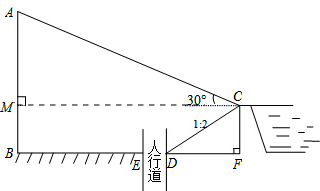
∵背水坡CD的坡度为i=1:2,
∴
=
,
∴DF=4.
∴CM=BF=BD+DF=14+4=18米;
(2)在Rt△AMC中,∵tan∠ACM=
,
∴AM=CM•tan∠ACM=18•tan30°=18×
=6
∴AB=AM+BM=6
+2≈12.239(m).
而BE=BD-DE=14-2=12(m).
∴AB>BE.故需封闭人行道DE.
∴BM=CF=2,BF=CM

∵背水坡CD的坡度为i=1:2,
∴
| CF |
| DF |
| 1 |
| 2 |
∴DF=4.
∴CM=BF=BD+DF=14+4=18米;
(2)在Rt△AMC中,∵tan∠ACM=
| AM |
| CM |
∴AM=CM•tan∠ACM=18•tan30°=18×
| ||
| 3 |
| 3 |
∴AB=AM+BM=6
| 3 |
而BE=BD-DE=14-2=12(m).
∴AB>BE.故需封闭人行道DE.
点评:本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
已知不等式组
的解集是x>2,则a的取值范围是( )
|
| A、a≤2 | B、a<2 |
| C、a=2 | D、a>2 |
 如图:△ABC为等边三角形,点D为△ABC内一点,且∠ADB=120°,把△ADB沿BD翻折,点A落在点E处,连接CE.
如图:△ABC为等边三角形,点D为△ABC内一点,且∠ADB=120°,把△ADB沿BD翻折,点A落在点E处,连接CE. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线交点的三角形)ABC的顶点A,B,C的坐标分别为(-3,2),(0,4),(0,2).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线交点的三角形)ABC的顶点A,B,C的坐标分别为(-3,2),(0,4),(0,2). 已知,如图,在Rt△ABC中,∠ACB=90°,点D为AB中点,连接CD.点E为边AC上一点,过点E作EF∥AB,交CD于点F,连接EB,取EB的中点G,连接DG、FG.
已知,如图,在Rt△ABC中,∠ACB=90°,点D为AB中点,连接CD.点E为边AC上一点,过点E作EF∥AB,交CD于点F,连接EB,取EB的中点G,连接DG、FG. 甲、乙二人同时从A地出发前往相距3000米的B地运送快递,其中甲的速度比乙快,二人途中均未停留.设甲乙二人相距y米,行进时间为x分钟,y与x之间的函数关系如图所示.请解决下列问题:
甲、乙二人同时从A地出发前往相距3000米的B地运送快递,其中甲的速度比乙快,二人途中均未停留.设甲乙二人相距y米,行进时间为x分钟,y与x之间的函数关系如图所示.请解决下列问题: