题目内容
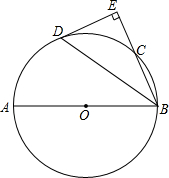 如图,AB是⊙O的直径,∠ABC的平分线BD交⊙O于D,过点D作DE⊥BC交BC的延长线于点E.
如图,AB是⊙O的直径,∠ABC的平分线BD交⊙O于D,过点D作DE⊥BC交BC的延长线于点E.(1)求证:DE是⊙O的切线;
(2)若AB=10,BD=8,求线段EC的长.
考点:切线的判定
专题:
分析:(1)如图,作辅助线;证明∠ODB=∠DBE;证明∠ODB+∠BDE=90°,即可解决问题.
(2)如图,作辅助线,求出AD,进而求出AF;证明△ADF≌△CED,即可解决问题.
(2)如图,作辅助线,求出AD,进而求出AF;证明△ADF≌△CED,即可解决问题.
解答: 解:(1)如图,连接OD;
解:(1)如图,连接OD;
∵OB=OD,
∴∠OBD=∠ODB;而BD平分∠ABE,
∴∠OBD=∠DBE,
∴∠ODB=∠DBE;而DE⊥BE,
∴∠BDE+∠DBE=90°,
∴∠ODB+∠BDE=90°,即∠ODE=90°,
∴DE是⊙O的切线.
(2)如图,连接AD、DC,过点D作DF⊥AB于点F;
∵BD平分∠ABE,DE⊥BE,
∴DE=DF;
∵AB是⊙O的直径,
∴∠ADB=90°,而AB=10,BD=8,
∴由勾股定理得:AD2=AB2-BD2=36,
由射影定理得:AD2=AF•AB,
∴AF=3.6;
∵∠ABD=∠EBD,
∴AD=DC;
在△ADF与△CED中,
,
∴△ADF≌△CED(HL),
∴EC=DF=3.6.
 解:(1)如图,连接OD;
解:(1)如图,连接OD;∵OB=OD,
∴∠OBD=∠ODB;而BD平分∠ABE,
∴∠OBD=∠DBE,
∴∠ODB=∠DBE;而DE⊥BE,
∴∠BDE+∠DBE=90°,
∴∠ODB+∠BDE=90°,即∠ODE=90°,
∴DE是⊙O的切线.
(2)如图,连接AD、DC,过点D作DF⊥AB于点F;
∵BD平分∠ABE,DE⊥BE,
∴DE=DF;
∵AB是⊙O的直径,
∴∠ADB=90°,而AB=10,BD=8,
∴由勾股定理得:AD2=AB2-BD2=36,
由射影定理得:AD2=AF•AB,
∴AF=3.6;
∵∠ABD=∠EBD,
∴AD=DC;
在△ADF与△CED中,
|
∴△ADF≌△CED(HL),
∴EC=DF=3.6.
点评:该题以圆为载体,以考查切线的判定、勾股定理、角平分线的性质、射影定理等重要几何知识点为核心构造而成;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
某校组织若干师生进行社会实践活动.若学校租用45座的客车x辆,则余下15人无座位;若租用60座的客车则可少租用1辆,则最后一辆还没坐满,那么乘坐最后一辆60座客车的人数是( )
| A、75-15x |
| B、135-15x |
| C、75+15x |
| D、135-60x |
下列运算中,正确的是( )
| A、4a-3a=1 |
| B、a•a2=a3 |
| C、3a6÷a3=3a2 |
| D、(ab3)3=a3b6 |
下列各对数中,数值相等的是( )
| A、-32与-23 |
| B、(-3)2与-32 |
| C、-23与(-2)3 |
| D、(-3×2)3与-3×23 |
若(x+a)(x+b)=x2+px+q,且p>0,q<0,那么a、b必须满足的条件是( )
| A、a、b都是正数 |
| B、a、b异号,且正数的绝对值较大 |
| C、a、b都是负数 |
| D、a、b异号,且负数的绝对值较大 |
已知等腰三角形一边长为4,周长为10,则另两边长分别为( )
| A、4,2 | B、3,3 |
| C、4,2或3,3 | D、以上都不对 |
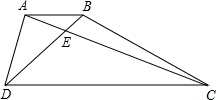 如图,在梯形ABCD中,AB∥CD,AC、BD相交于点E,且CE:AE=3:1,S△ADE=6cm2,试求:
如图,在梯形ABCD中,AB∥CD,AC、BD相交于点E,且CE:AE=3:1,S△ADE=6cm2,试求: