题目内容
9.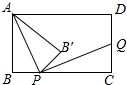 如图,在矩形ABCD中,AB=6,BC=8,点P是BC边上的一个动点(点P与点B、C都不重合),现将△PAB沿直线PA折叠,使点B落到点B′处;过点P作∠CPB′的角平分线交CD于点Q.设BP=x,CQ=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,在矩形ABCD中,AB=6,BC=8,点P是BC边上的一个动点(点P与点B、C都不重合),现将△PAB沿直线PA折叠,使点B落到点B′处;过点P作∠CPB′的角平分线交CD于点Q.设BP=x,CQ=y,则下列图象中,能表示y与x的函数关系的图象大致是( )| A. | 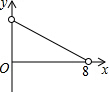 | B. | 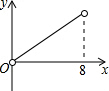 | C. | 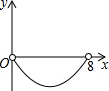 | D. | 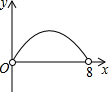 |
分析 只要证明△ABP∽△PCQ得$\frac{AB}{PC}$=$\frac{PB}{CQ}$即可解决问题.
解答 解:∵△ABP沿PA翻折得到△AB′P,
∴∠APB=∠APB′,
∵PQ平分∠B′PC,
∴∠B′PQ=∠CPQ,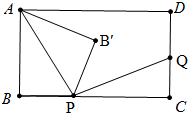
∴∠APB′+∠QPB′=$\frac{1}{2}$×180°=90°,
∵∠C=90°,
∴∠CPQ+∠CQP=90°,
∴∠APB=∠CQP,
又∵∠B=∠C=90°,
∴△ABP∽△PCQ,
∴$\frac{AB}{PC}$=$\frac{PB}{CQ}$,
∵BP=x,CQ=y,矩形ABCD中,BC=8,AB=6,
∴CP=8-x,CD=AB=6,
∴$\frac{6}{8-x}$=$\frac{x}{y}$,
∴y=$\frac{1}{6}$x(8-x)=-$\frac{1}{6}$x2+$\frac{4}{3}$x.
∴图象是抛物线,开口向下.
故选D.
点评 本题考查矩形的性质、翻折变换、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,属于中考常考题型.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,在三角形ABC中,AB∥DE,AD⊥BC,∠BAC=90°,与∠DAC相等的角(不包括∠DAC本身)有( )
如图,在三角形ABC中,AB∥DE,AD⊥BC,∠BAC=90°,与∠DAC相等的角(不包括∠DAC本身)有( )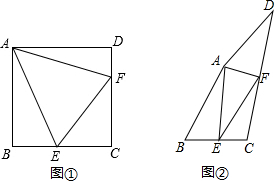
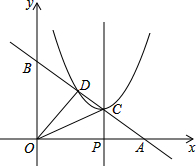 已知直线y=-$\frac{3}{4}x+3$分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒,以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D,设△COD的OC边上的高为h,当t=$\frac{36}{25}$时,h的值最大.
已知直线y=-$\frac{3}{4}x+3$分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒,以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D,设△COD的OC边上的高为h,当t=$\frac{36}{25}$时,h的值最大.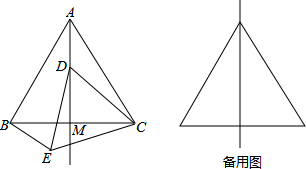
 如图,⊙O是△ABC的外接圆,∠A=60°,过点C作⊙O的切线,交射线BO于点E.
如图,⊙O是△ABC的外接圆,∠A=60°,过点C作⊙O的切线,交射线BO于点E.