题目内容
2.如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边且在CD的下方作等边△CDE,连结BE.(1)填空:∠ACB=60度;
(2)当点D在线段AM上(点D不运动到点A)时,试求出$\frac{AD}{BE}$的值;
(3)当点D在射线AM上点M下方时时,$\frac{AD}{BE}$的值是否发生改变,并说出理由.
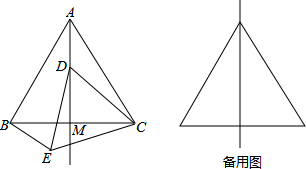
分析 (1)根据等边三角形的每一个内角都等于60°解答;
(2)根据等边三角形的三条边都相等可得AC=BC,CD=CE,每一个内角都等于60°可得∠ACB=∠DCE=60°,再求出∠ACD=∠BCE,然后利用“边角边”证明△ACD和△BCE全等,根据全等三角形对应边相等可得AD=BE,从而得解;
(3)作出图形,然后与(2)同理求解即可.
解答 (1)解:∵△ABC是等边三角形,
∴∠ACB=60°;
故答案为:60;
(2)解:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∵∠ACD+∠BCD=∠ACB,
∠BCE+∠BCD=∠DCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),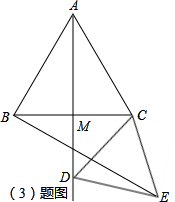
∴AD=BE,
∴$\frac{AD}{BE}$=1;
(3)解:点D在射线AM上点M下方时,$\frac{AD}{BE}$的值不会发生改变.
理由如下:如图,∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∵∠ACD-∠BCD=∠ACB,
∠BCE-∠BCD=∠DCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∴$\frac{AD}{BE}$=1.
点评 本题考查了全等三角形的判定与性质,等边三角形的性质,熟练掌握各性质并确定出全等三角形是解题的关键.

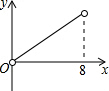
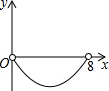
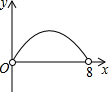
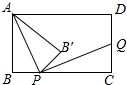 如图,在矩形ABCD中,AB=6,BC=8,点P是BC边上的一个动点(点P与点B、C都不重合),现将△PAB沿直线PA折叠,使点B落到点B′处;过点P作∠CPB′的角平分线交CD于点Q.设BP=x,CQ=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,在矩形ABCD中,AB=6,BC=8,点P是BC边上的一个动点(点P与点B、C都不重合),现将△PAB沿直线PA折叠,使点B落到点B′处;过点P作∠CPB′的角平分线交CD于点Q.设BP=x,CQ=y,则下列图象中,能表示y与x的函数关系的图象大致是( )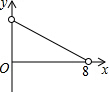
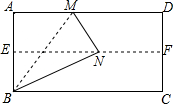 如果是我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法(如图):
如果是我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法(如图):