题目内容
5.若a<b,用“>”或“<”填空(1)a-4<b-4
(2)$\frac{a}{5}$<$\frac{b}{5}$
(3)-2a>-2b.
分析 (1)根据不等式的基本性质,两边同时-4,不等号的方向不变即可解答:
(2)根据不等式的基本性质,两边同时除以5,不等号的方向不变解答即可:
(3)根据不等式的基本性质,两边同时乘以-2,不等号的方向改变即可解答.
解答 解:(1)根据不等式的基本性质1可得:a-4<b-4;
(2)根据不等式的基本性质2可得:$\frac{a}{5}$<$\frac{b}{5}$;
(3)根据不等式的基本性质3可得:-2a>-2b,
故答案为<,<,>.
点评 本题主要考查了不等式的基本性质.不等式的基本性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
10.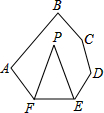 如图,在六边形ABCDEF中,∠A+∠B+∠C+∠D=460°,FP、EP分别平分∠AFE,∠FED,则∠P的度数是( )
如图,在六边形ABCDEF中,∠A+∠B+∠C+∠D=460°,FP、EP分别平分∠AFE,∠FED,则∠P的度数是( )
 如图,在六边形ABCDEF中,∠A+∠B+∠C+∠D=460°,FP、EP分别平分∠AFE,∠FED,则∠P的度数是( )
如图,在六边形ABCDEF中,∠A+∠B+∠C+∠D=460°,FP、EP分别平分∠AFE,∠FED,则∠P的度数是( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
17.如果ax<a的解是x>1,那么a必须满足( )
| A. | a>0 | B. | a<0 | C. | a>1 | D. | a<1 |
14.已知ab=-5,a-b=6,则a2+b2=( )
| A. | 13 | B. | 19 | C. | 26 | D. | 37 |
15.解为x=-3的方程是( )
| A. | 3x-2=-7 | B. | 3x+2=-11 | C. | 2x+6=0 | D. | x-3=0 |
