题目内容
若（x2-px+3）（x+2）的乘积中不含x2项，则（ ）
| A、p=2 | B、p=±2 |
| C、p=-2 | D、无法确定 |
考点：多项式乘多项式
专题：
分析：根据多项式乘以多项式法则展开，合并后根据对应的x2的系数相等得出2+p=0，求出即可．
解答：解：（x2-px+3）（x+2）=x3-px2+3x+2x2-2px+6=x3+（-p+2）x2+（-2p+3）x+6，
因为乘积中不含x2项，则-p+2=0，
解得p=2．
故选：A．
因为乘积中不含x2项，则-p+2=0，
解得p=2．
故选：A．
点评：本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．
练习册系列答案
相关题目
如果直角三角形三边长为三个连续的自然数，则这三边可能的是（ ）
| A、1、2、3 |
| B、2、3、4 |
| C、3、4、5 |
| D、4、5、6 |
同一平面内的四条直线a、b、c、d满足下列条件：a⊥b，b⊥c，c⊥d，则下列各式成立的是（ ）
| A、a∥b | B、b∥c |
| C、a⊥d | D、b⊥d |
如图，直线AB∥CD，下列关于∠B、∠D、∠E关系中，正确的是（ ）| A、∠B+∠D+∠E=90° |
| B、∠B+∠D+∠E=180° |
| C、∠B=∠E-∠D |
| D、∠B-∠D=∠E |
若x+y=0，则下列各式不成立的是（ ）
| A、x2-y2=0 | ||||||
B、
| ||||||
C、
| ||||||
D、
|
多边形的每个内角都是120°，则从这个多边形的某一个顶点出发引出的对角线共有多少条（ ）
| A、10条 | B、9条 | C、3条 | D、4条 |
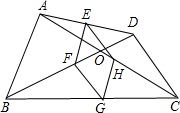已知：如图，四边形ABCD中，对角线相交于点O、E、F、G、H分别是AD、BD、BC、AC的中点．