题目内容
9.某工厂生产一种长与宽比例为3:2的矩形装饰板,其成本与矩形的面积成正比,已知宽为30时的成本为270元,则成本C与装饰板宽d的函数关系式是C=$\frac{3}{10}$d2.分析 首先表示成本C与面积的关系式,再根据长与宽比例为3:2,表示出若宽d,则长为$\frac{3}{2}$d,然后利用d表示面积,再列函数关系式即可.
解答 解:∵长与宽比例为3:2,
∴宽为30时,长为45,
∵成本与矩形的面积成正比,
∴设C=kS,
∵宽为30时的成本为270元,
∴270=30×45×k,
解得:k=$\frac{1}{5}$,
∴C=$\frac{1}{5}$S,
若宽d,则长为$\frac{3}{2}$d,
S=$\frac{3}{2}$d2,
∴C=$\frac{3}{10}$d2,
故答案为:C=$\frac{3}{10}$d2.
点评 此题主要考查了根据实际问题列函数关系式,关键是掌握正比例函数是y=kx(k≠0)的形式.

练习册系列答案
相关题目
19.不等式$\left\{\begin{array}{l}{2x-1>-3}\\{4-\frac{1}{3}x≥2}\end{array}\right.$的解集是( )
| A. | x≥6 | B. | -1≤x<6 | C. | -1<x≤6 | D. | x<-1 |
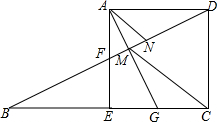 如图,在正方形ADCE中,F为AE中点,DF交CE的延长线于B点,CM∥AN,交DF于M,N.
如图,在正方形ADCE中,F为AE中点,DF交CE的延长线于B点,CM∥AN,交DF于M,N.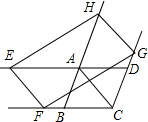 如图,直线EF与?ABCD的对角线AC平行,分别交DA,CB的延长线于点E,F,直线GH与AC平行,分别交CD,BA的延长线于点G,H,则EF与HG的关系是EF=HG,EF∥HG.
如图,直线EF与?ABCD的对角线AC平行,分别交DA,CB的延长线于点E,F,直线GH与AC平行,分别交CD,BA的延长线于点G,H,则EF与HG的关系是EF=HG,EF∥HG. 如图,点D、E分别在△ABC边BC、AC上,连接线段AD、BE交于点F,若AE:EC=1:3,BD:DC=2:3,则EF:FB=$\frac{3}{8}$.
如图,点D、E分别在△ABC边BC、AC上,连接线段AD、BE交于点F,若AE:EC=1:3,BD:DC=2:3,则EF:FB=$\frac{3}{8}$.