题目内容
1.已知关于x的方程4x-a=1与$\frac{1}{3}$x+(a+2)=3x+2的解相同,求a的值.分析 先分别解关于x的方程4x-a=1与$\frac{1}{3}$x+(a+2)=3x+2,再根据两个方程的解相同列出关于a的方程,求解即可.
解答 解:解方程4x-a=1,得x=$\frac{a+1}{4}$,
解方程$\frac{1}{3}$x+(a+2)=3x+2,得x=$\frac{3}{8}$a,
∵关于x的方程4x-a=1与$\frac{1}{3}$x+(a+2)=3x+2的解相同,
∴$\frac{a+1}{4}$=$\frac{3}{8}$a,
解得a=2.
故所求a的值为2.
点评 本题考查了同解方程的定义:如果两个方程的解相同,那么这两个方程叫做同解方程.解题的关键是能够求解关于x的方程,根据同解的定义建立关于a的方程.

练习册系列答案
相关题目
16.下列命题:
①圆上任意两点间的部分叫弦
②长度相等的弧叫等弧
③在同圆或等圆中相等的弦所对的弧相等
④平分弦的直径垂直于弦
⑤半圆或直径所对的圆周角是直角
正确的个数是( )个.
①圆上任意两点间的部分叫弦
②长度相等的弧叫等弧
③在同圆或等圆中相等的弦所对的弧相等
④平分弦的直径垂直于弦
⑤半圆或直径所对的圆周角是直角
正确的个数是( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.若x=1是关于x的方程x+1=-x-1+2m的解,则m=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
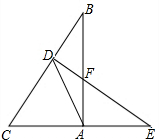 如图,△ABC中,∠BAC=90°,点D为BC上一点,且∠C=∠DAC,DE⊥BC交AB于F,交CA的延长线于E.
如图,△ABC中,∠BAC=90°,点D为BC上一点,且∠C=∠DAC,DE⊥BC交AB于F,交CA的延长线于E.