题目内容
19.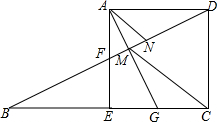 如图,在正方形ADCE中,F为AE中点,DF交CE的延长线于B点,CM∥AN,交DF于M,N.
如图,在正方形ADCE中,F为AE中点,DF交CE的延长线于B点,CM∥AN,交DF于M,N.(1)求证:△CDM∽△AFN;
(2)若$\frac{FM}{DN}$=$\frac{2}{7}$,求$\frac{AM}{MC}$的值.
分析 (1)由四边形ADCE是正方形,得到AE∥CD,根据平行线的性质得到∠AFN=∠CDM,∠ANM=∠CMD,即可得到结论;
(2)根据相似三角形的性质得到$\frac{AF}{CD}=\frac{FN}{DM}$设FM=2x,DN=7x,于是得到$\frac{AF}{AE}=\frac{2x+MN}{7x+MN}=\frac{1}{2}$,根据全等三角形的性质得到DF=BF=12x,求得DM=10x,BM=14x,然后根据相似三角形的性质即可得到结论.
解答 (1)证明:∵四边形ADCE是正方形,
∴AE∥CD,
∴∠AFN=∠CDM,
∵AN∥CM,
∴∠ANM=∠CMD,
∴△CDM∽△AFN;
(2)解:∵△CDM∽△AFN,
∴$\frac{AF}{CD}=\frac{FN}{DM}$,∵$\frac{FM}{DN}$=$\frac{2}{7}$,
∴设FM=2x,DN=7x,
∵AE=CD,F为AE中点,
∴$\frac{AF}{AE}=\frac{2x+MN}{7x+MN}=\frac{1}{2}$,
∴MN=3x,
在△ADF与△BEF中,$\left\{\begin{array}{l}{∠DAF=∠FEB=90°}\\{AF=EF}\\{∠AFD=∠EFB}\end{array}\right.$,
∴△ADF≌△BEF,
∴DF=BF=12x,∴DM=10x,BM=14x,
∵AD∥BC,
∴△ADM∽△BMG,
∴$\frac{AM}{MG}=\frac{DM}{BM}$=$\frac{5}{7}$.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,正方形的性质,平行线的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.多项式-π2x5-2x3y3+3x-5的次数是( )
| A. | 3 | B. | 5 | C. | 6 | D. | 7 |
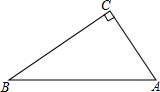 如图,已知△ABC中,∠ACB=90°,AC=3,BC=5,M为AB的中点.
如图,已知△ABC中,∠ACB=90°,AC=3,BC=5,M为AB的中点.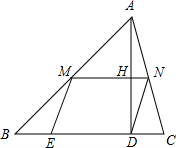 如图,在△ABC中,AD⊥BC,垂足为D,?DEMN的一边DE在BC上,另两个顶点M,N分别在AB,AC上,MN交AD于H.当ND=NC时,求$\frac{AH}{AD}$的值.
如图,在△ABC中,AD⊥BC,垂足为D,?DEMN的一边DE在BC上,另两个顶点M,N分别在AB,AC上,MN交AD于H.当ND=NC时,求$\frac{AH}{AD}$的值.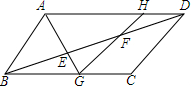 如图,E,F是平行四边形ABCD的对角线AC上的三等分点,连接AE并延长,交BC于点G,连接GF并延长,交AD于点H,若AD=12,求DH的长.
如图,E,F是平行四边形ABCD的对角线AC上的三等分点,连接AE并延长,交BC于点G,连接GF并延长,交AD于点H,若AD=12,求DH的长.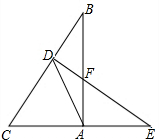 如图,△ABC中,∠BAC=90°,点D为BC上一点,且∠C=∠DAC,DE⊥BC交AB于F,交CA的延长线于E.
如图,△ABC中,∠BAC=90°,点D为BC上一点,且∠C=∠DAC,DE⊥BC交AB于F,交CA的延长线于E.