题目内容

19．不等式$\left\{\begin{array}{l}{2x-1＞-3}\\{4-\frac{1}{3}x≥2}\end{array}\right.$的解集是（　　）
A．x≥6B．-1≤x＜6C．-1＜x≤6D．x＜-1

分析 首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集．

解答 解：$\left\{\begin{array}{l}{2x-1＞-3…①}\\{4-\frac{1}{3}x≥2…②}\end{array}\right.$，
解①得x＞-1，
解②得x≤6．
则不等式组的解集是：-1＜x≤6．
故选C．

点评 本题考查了一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．

练习册系列答案
相关题目
9．某工厂生产一种长与宽比例为3：2的矩形装饰板，其成本与矩形的面积成正比，已知宽为30时的成本为270元，则成本C与装饰板宽d的函数关系式是C=$\frac{3}{10}$d2．
10．解方程：
（1）5（x-5）+2x=-4；                    
（2）$\frac{x}{3}$=1-$\frac{x-1}{5}$．
7．解下列分式方程：
（1）$\frac{x}{x-2}$=$\frac{x-2}{x+2}$      
（2）$\frac{4x+10}{3x-6}$-$\frac{5x-4}{x-2}$=1．
14．已知xm+ny2余xym-n的和是单项式，则可列得二元一次方程组$\left\{\begin{array}{l}{m+n=1}\\{m-n=2}\end{array}\right.$．
4．阅读理解：
材料一、对于二次三项式x2+2ax+a2可以直接用公式法分解为（x+a）2的形式，但对于二次三项式x4-3x2+1，就不能直接用公式法了，我们可以把二次三项式x4-3x2+1中3x2拆成2x2+x2，于是
有x4-3x2+1=x4-2x2-x2+1=x4-2x2+1-x2=（x2-1）2-x2=（x2-x-1）（x2+x-1）．
像上面这样把二次三项式分解因式的方法叫拆项法．
（1）请用上述方法对多项x4-7x2+9进行因式分解；
材料二、把一个分式写成两个分式的和叫做把这个分式表示成部分分式，如何将$\frac{1-3x}{{x}^{2}-1}$表示成部分分式？
设分式$\frac{1-3x}{{x}^{2}-1}$=$\frac{m}{x-1}$$+\frac{n}{x+1}$，将等式的右边通分得：$\frac{m（x+1）+n（x-1）}{（x+1）（x-1）}$=$\frac{（m+n）x+m-n}{（x+1）（x-1）}$
由$\frac{1-3x}{{x}^{2}-1}$=$\frac{（m+n）x+m-n}{（x-1）（x+1）}$得$\left\{\begin{array}{l}{m+n=-3}\\{m-n=1}\end{array}\right.$解得$\left\{\begin{array}{l}{m=-1}\\{n=-2}\end{array}\right.$，所以$\frac{1-3x}{{x}^{2}-1}$=$\frac{-1}{x-1}$$+\frac{-2}{x+1}$．
（2）请用上述方法将分式$\frac{4x-3}{（2x+1）（x-2）}$写成部分分式的和的形式．
11．（1）问题背景：
如图（1），在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°．E，F分别是BC，CD上的点．且∠EAF=60°，探索EF，BE，FD的数量关系，王岩和张放两位同学探索的思路虽然不尽相同，但都得出了正确的结论．
     王岩是这样想的：把△ABE绕着点A逆时针旋转到使AB与AD重合，得△ADG，并确定点F，D，G在一条直线上，再证明△AEF≌AGF…
     张放是这样想的：延长FD到点G，使DG=BE，连接AG，先证明△ABE≌△ADG，△AEF≌△AGF…
他们得出的结论是EF=BE+DF．
（2）探索延伸：
如图（2），若在四边形ABCD中，AB=AD，∠B+∠D=180°．E，F分别是BC，CD上的点，且∠EAF=$\frac{1}{2}$∠BAD，（1）中的结论是否仍然成立？并说明理由；
（3）实际应用：
如图（3），在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心（O处）南偏东70°的B处，并且两舰艇到指挥中心的距离都是90海里，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，同时，舰艇乙沿着射线BM的方向（∠OBF=120°），以14海里/小时的速度前进1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且舰艇乙在指挥中心南偏东80°，试问，两舰艇E，F之间的距离是否符合（2）的条件？如果符合，请求出两舰艇之间的距离（画出辅助线）；如果不符合，请说明理由．
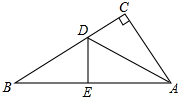8．如图，在Rt△ABC中，∠C=90°，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合．若CD=6，BD=10，求AC长．
9．已知不等式$\frac{1+x}{2}$＜$\frac{2x-1}{3}$的最小整数解是方程3（x-a）-1=8的解，求a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网