题目内容
3.在?ABCD中,AD=BD,BE是AD边上的高,∠EBD=20°,则∠A的度数为55°或35°.分析 首先求出∠ADB的度数,再利用三角形内角和定理以及等腰三角形的性质,得出∠A的度数.
解答 解:情形一:当E点在线段AD上时,如图所示,
∵BE是AD边上的高,∠EBD=20°,
∴∠ADB=90°-20°=70°,
∵AD=BD,
∴∠A=∠ABD=$\frac{180°-70°}{2}$=55°.
情形二:当E点在AD的延长线上时,如图所示,
∵BE是AD边上的高,∠EBD=20°,
∴∠BDE=70°,
∵AD=BD,
∴∠A=∠ABD=$\frac{1}{2}$∠BDE=$\frac{1}{2}$×70°=35°.
故答案为:55°或35°.
点评 此题主要考查了平行四边形的性质以及等腰三角形的性质等知识,得出∠ADB的度数是解题关键.

练习册系列答案
相关题目
14. 如图,AB为⊙O直径,已知∠DCB=20°,则∠DBA为( )
如图,AB为⊙O直径,已知∠DCB=20°,则∠DBA为( )
 如图,AB为⊙O直径,已知∠DCB=20°,则∠DBA为( )
如图,AB为⊙O直径,已知∠DCB=20°,则∠DBA为( )| A. | 50° | B. | 20° | C. | 60° | D. | 70° |
11.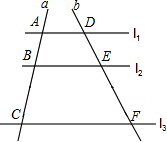 如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=4,则EF的长是( )
如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=4,则EF的长是( )
 如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=4,则EF的长是( )
如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=4,则EF的长是( )| A. | $\frac{8}{3}$ | B. | $\frac{20}{3}$ | C. | 6 | D. | 10 |
18.下列说法中正确的是( )
| A. | “任意画出一个等边三角形,它是轴对称图形”是随机事件 | |
| B. | “任意画出一个平行四边形,它是中心对称图形”是必然事件 | |
| C. | “概率为0.0001的事件”是不可能事件 | |
| D. | 任意掷一枚质地均匀的硬币10次,正面向上的一定是5次 |
13.反比例函数y=$\frac{1}{x}$的图象是( )
| A. | 线段 | B. | 直线 | C. | 抛物线 | D. | 双曲线 |