题目内容
15.现有两个不透明的盒子,其中一个装有标号分别为1,2的两张卡片,另一个装有标号分别为1,2,3的三张卡片,卡片除标号外其他均相同.若从两个盒子中各随机抽取一张卡片,则两张卡片标号恰好相同的概率是$\frac{1}{3}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两张卡片标号恰好相同的情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有6种等可能的结果,两张卡片标号恰好相同的有2种情况,
∴两张卡片标号恰好相同的概率是:$\frac{2}{6}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
10.我们解一元二次方程3x2-6x=0时,可以运用因式分解法,将此方程化为3x(x-2)=0,从而得到两个一元一次方程:3x=0或x-2=0,进而得到原方程的解为x1=0,x2=2.这种解法体现的数学思想是( )
| A. | 转化思想 | B. | 函数思想 | C. | 数形结合思想 | D. | 公理化思想 |
20.袋中有5个红球、4个白球、3个黄球,每一个球除颜色外都相同,从袋中任意摸出一个球是白球的概率( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{12}$ | D. | $\frac{7}{12}$ |
4. 已知,AC∥ED,∠C=26°,∠CBE=37°,则∠BED的度数是( )
已知,AC∥ED,∠C=26°,∠CBE=37°,则∠BED的度数是( )
 已知,AC∥ED,∠C=26°,∠CBE=37°,则∠BED的度数是( )
已知,AC∥ED,∠C=26°,∠CBE=37°,则∠BED的度数是( )| A. | 53° | B. | 63° | C. | 73° | D. | 83° |
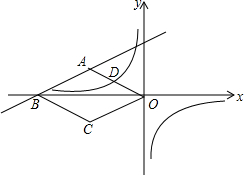 如图,在平面直角坐标系中,四边形ABCO是菱形,B、O在x轴负半轴上,AO=$\sqrt{5}$,tan∠AOB=$\frac{1}{2}$,一次函数y=k1x+b的图象过A、B两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象过OA的中点D.
如图,在平面直角坐标系中,四边形ABCO是菱形,B、O在x轴负半轴上,AO=$\sqrt{5}$,tan∠AOB=$\frac{1}{2}$,一次函数y=k1x+b的图象过A、B两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象过OA的中点D.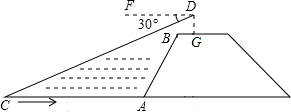 如图,小华站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角是∠FDC=30°,若小华的眼睛与地面的距离是1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=8米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长为8$\sqrt{3}$-5.5米.(结果保留根号)
如图,小华站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角是∠FDC=30°,若小华的眼睛与地面的距离是1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=8米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长为8$\sqrt{3}$-5.5米.(结果保留根号)