题目内容
6.已知关于x的方程(b-c)x2+2(a-b)x+b-a=0有两个相等的实数根,则以a、b、c为三边长的三角形的形状一定是等腰三角形.分析 根据二次项系数非零结合根的判别式△=0,即可得出a=c≠b,从而得出以a、b、c为三边长的三角形为等腰三角形.
解答 解:∵关于x的方程(b-c)x2+2(a-b)x+b-a=0有两个相等的实数根,
∴$\left\{\begin{array}{l}{b-c≠0}\\{△=[2(a-b)]^{2}-4(b-c)(b-a)=0}\end{array}\right.$,
解得:a=c≠b,
∴以a、b、c为三边长的三角形为等腰三角形.
故答案为:等腰三角形.
点评 本题考查了根的判别式,牢记“当△=0时,方程有两个相等的实数根”是解题的关键.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
14.若∠A,∠B互为补角,且∠A=36°,则∠B等于( )
| A. | 134° | B. | 64° | C. | 144° | D. | 54° |
1.方程x2+17=8x的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
10.已知点P(2-a,a)在平面直角坐标系的第四象限内,则直线y=ax+3不经过第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
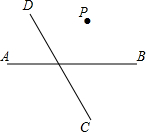 读句画图,如图直线AB与直线CD相交于C
读句画图,如图直线AB与直线CD相交于C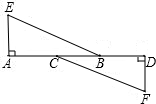 如图,点A,B,C,D在同一直线上,AE⊥AD,FD⊥AD,垂足分别为A,D,AE=DF,BE=CF,求证:AC=DB.
如图,点A,B,C,D在同一直线上,AE⊥AD,FD⊥AD,垂足分别为A,D,AE=DF,BE=CF,求证:AC=DB.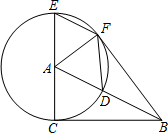 如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.
如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF. 如图,射线OA的方向是西南方向,射线OB的方向是北偏西70°,则∠AOB=65°.
如图,射线OA的方向是西南方向,射线OB的方向是北偏西70°,则∠AOB=65°.