题目内容
16.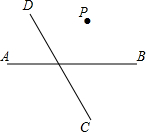 读句画图,如图直线AB与直线CD相交于C
读句画图,如图直线AB与直线CD相交于C(1)过点P作PQ∥CD,交AB于Q;
(2)过点P作PR⊥CD于R;
(3)若∠DCB=120°,猜想∠PQC的度数,并说明理由.
分析 (1)、(2)利用几何语言画出对应的几何图形;
(3)根据平行线的性质计算.
解答 解:(1)如图,PQ为所作;
(2)如图,PR为所作;
(3)∠PQC的度数为60°.理由如下:
∵CD∥PQ,
∴∠DCB+∠PQC=180°,
∴∠PQC=180°-120°=60°.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行线的性质.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
6.计算(-0.25)2015×42015的结果是( )
| A. | -1 | B. | 1 | C. | 0.25 | D. | 45000 |
1.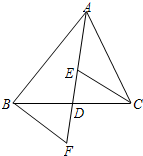 如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE,下列说法:①CE=BF;②BF∥CE;③△BDF≌△CDE.其中正确的有( )
如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE,下列说法:①CE=BF;②BF∥CE;③△BDF≌△CDE.其中正确的有( )
 如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE,下列说法:①CE=BF;②BF∥CE;③△BDF≌△CDE.其中正确的有( )
如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE,下列说法:①CE=BF;②BF∥CE;③△BDF≌△CDE.其中正确的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
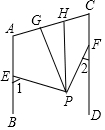 如图:AB∥CD,PG平分∠EPF,PH∥CD,下列结论:
如图:AB∥CD,PG平分∠EPF,PH∥CD,下列结论: