题目内容
17．已知点M（1，a）和点N（2，b）是一次函数y=-$\frac{1}{2}$x-1的图象上的两点，则a＞b（填“＞”或“=”或“＜”）．分析 由k=-$\frac{1}{2}$＜0结合一次函数的性质即可得出该函数为减函数，再结合1＜2即可得出结论．
解答 解：∵k=-$\frac{1}{2}$＜0，
∴一次函数y随x增大而减小，
∵1＜2，
∴a＞b．
故答案为＞．
点评 本题考查了一次函数的性质，解题的关键确定一次函数的增减性．
练习册系列答案
名校课堂系列答案
相关题目
5．
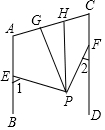如图：AB∥CD，PG平分∠EPF，PH∥CD，下列结论：
①∠1+∠2=2∠EPG； ②∠EPG-∠GPH=∠2；
③∠FPH=∠GPH； ④设∠1＞∠2，则$\frac{∠1-∠2}{∠GPH}$为定值．
其中正确结论的个数是（ ）
如图：AB∥CD，PG平分∠EPF，PH∥CD，下列结论：①∠1+∠2=2∠EPG； ②∠EPG-∠GPH=∠2；
③∠FPH=∠GPH； ④设∠1＞∠2，则$\frac{∠1-∠2}{∠GPH}$为定值．
其中正确结论的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
2．在下列命题中，是假命题的是（ ）
| A． | 有一个角是直角的平行四边形是矩形 | |
| B． | 一组邻边相等的矩形是正方形 | |
| C． | 一组对边平行且相等的四边形是平行四边形 | |
| D． | 有两组邻边相等的四边形是菱形 |