题目内容
19.已知α、β是方程$\sqrt{2}$x2+$\sqrt{6}$x-1=0的两个实根,则α2+β2=( )| A. | 3-$\sqrt{2}$ | B. | 3+$\sqrt{2}$ | C. | -3-$\sqrt{2}$ | D. | -3+$\sqrt{2}$ |
分析 由韦达定理可得α+β=-$\sqrt{3}$、αβ=-$\frac{\sqrt{2}}{2}$,代入到α2+β2=(α+β)2-2αβ中计算可得.
解答 解:根据题意得,α+β=-$\frac{\sqrt{6}}{\sqrt{2}}$=-$\sqrt{3}$,αβ=-$\frac{1}{\sqrt{2}}$=-$\frac{\sqrt{2}}{2}$,
则α2+β2=(α+β)2-2αβ
=(-$\sqrt{3}$)2-2×(-$\frac{\sqrt{2}}{2}$)
=3+$\sqrt{2}$.
故选:B.
点评 本题主要考查一元二次方程根与系数的关系,掌握根与系数的关系是根本,待求代数式变形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.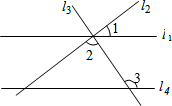 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )
 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )| A. | 26° | B. | 36° | C. | 46° | D. | 56° |
10.下列运算正确的是( )
| A. | a0=1 | B. | $\sqrt{9}$=±3 | C. | (ab)2=ab2 | D. | (-a2)3=-a6 |
7. 已知一次函数y=ax+c的图象如图所示,那么一元二次方程ax2+bx+c=0的根的情况是( )
已知一次函数y=ax+c的图象如图所示,那么一元二次方程ax2+bx+c=0的根的情况是( )
 已知一次函数y=ax+c的图象如图所示,那么一元二次方程ax2+bx+c=0的根的情况是( )
已知一次函数y=ax+c的图象如图所示,那么一元二次方程ax2+bx+c=0的根的情况是( )| A. | 方程有两个不相等的实数根 | B. | 方程有两个相等的实数根 | ||
| C. | 方程没有实数根 | D. | 无法判断 |
14.马大哈做题很快,但经常不仔细思考,所以往往错误率很高,有一次做了四个题,但只做对了一个,他做对的是( )
| A. | a8÷a4=a2 | B. | a3•a4=a12 | C. | $\sqrt{4}$=±2 | D. | 2x3•x2=2x5 |
11. 如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )
如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )
 如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )
如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )| A. | 100° | B. | 90° | C. | 80° | D. | 70° |
8.对于方程y2+5y-1=0,下列说法正确的是( )
| A. | 方程无实数根 | B. | 方程有两个相等的实数根 | ||
| C. | 方程有两个不相等的实数根 | D. | 方程的根无法确定 |
6.$\sqrt{16}$的算术平方根是( )
| A. | 4和-4 | B. | 2和-2 | C. | 4 | D. | 2 |
 “瓦当”是中国古代用以装饰美化建筑物檐头的建筑附件,其图案各式各样,属于中国特有的文化艺术遗产.下列“瓦当”的图案中,是轴对称图形的为( )
“瓦当”是中国古代用以装饰美化建筑物檐头的建筑附件,其图案各式各样,属于中国特有的文化艺术遗产.下列“瓦当”的图案中,是轴对称图形的为( )


