题目内容
10.(1)如图1,点A,B,E不在同一条直线上,△ABC与△ADE都是等边三角形,连结BD、CE,请你猜想BD与CE的大小关系,请说明理由;(2)如图2,如果把两个等边三角形改成两个等腰直角△ABC与△ADE,其他条件不变!那么CE=BD成立吗?(直接写出答案);
(3)如图3,如果把两个等边三角形改成两个正方形,即正方形ABCD,正方形AEFG(正方形的四条边相等,四个角都是直角),连结BE,过点A作BE的垂线,交BE于点H,过点D、G分别作DM⊥AH,GN⊥AH,垂足分别为点N、M,猜想DM和NG的大小关系,并证明你的结论.
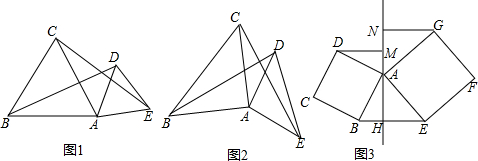
分析 (1)据等边三角形边长相等的性质和各内角为60°的性质可求得△ABD≌△ACE,根据全等三角形对应边相等的性质即可求得CE=BD.
(2)证明方法和(1)一样,利用SAS证得△ABD≌△ACE,得出BD=CE;
(3)首先利用AAS证得△ABH≌△DAM,得出DM=AH,同理证得△AHE≌△ANGA,得出NG=AH,推出DM=NG.
解答 解:(1)BD=CE.
∵△ABC、△ADE均为等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
∵在△ABD和△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠ACE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△CAE,
∴BD=CE.
(2)BD=CE.
∵△ABC、△ADE均为等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
∵在△ABD和△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠ACE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△CAE,
∴BD=CE.
(3)DM=NG.
∵正方形ABCD,正方形AEFG,
∴AB=AD,AG=AE,∠BAD=∠GAE=90°,
∵DM⊥AH,GN⊥AH,AH⊥BE,
∴∠AHB=∠AHE=∠DMA=∠GAN=90°,
∴∠DAM=∠ABH,∠NAG=∠AEH,
在△ABH和△ADM中,△AEH和△AGN中
$\left\{\begin{array}{l}{∠ABH=∠AMD}\\{∠ABH=∠DAM}\\{AB=AD}\end{array}\right.$,$\left\{\begin{array}{l}{∠AHE=∠ANG}\\{∠AEH=∠NAG}\\{AE=AG}\end{array}\right.$,
∴△ABH≌△ADM,△AEH≌△AGN,
∴DM=AH,NG=AH,
∴DM=NG.
点评 此题考查全等三角形的判定与性质,等边三角形,等腰直角三角形,正方形的性质,掌握三角形全等的判定方法是解决问题的关键.

 名校课堂系列答案
名校课堂系列答案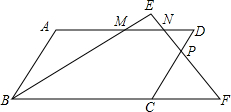 如图,在?ABCD中,M是AD的中点,N是MD的中点,点P在CD上,PN分别与BM、BC的延长线交于点E、F,且DP:PC=1:2.求EN:EF的值.
如图,在?ABCD中,M是AD的中点,N是MD的中点,点P在CD上,PN分别与BM、BC的延长线交于点E、F,且DP:PC=1:2.求EN:EF的值. 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-2,1),B(1,n)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-2,1),B(1,n)两点.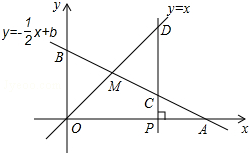 如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M(2,2),在x轴上有一动点P(a,0),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.
如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M(2,2),在x轴上有一动点P(a,0),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.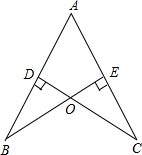 如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O.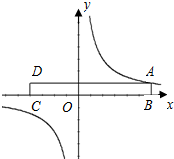 如图,将一张长方形的纸片ABCD沿x轴摆放,顶点A(6,1)恰好落在某双曲线上.现在AD边上找一点E,使得将纸片的右半部分沿OE所在直线折叠后,点A恰好还落在此双曲线上,则满足条件的点E的坐标为(1,1)(-1,1).
如图,将一张长方形的纸片ABCD沿x轴摆放,顶点A(6,1)恰好落在某双曲线上.现在AD边上找一点E,使得将纸片的右半部分沿OE所在直线折叠后,点A恰好还落在此双曲线上,则满足条件的点E的坐标为(1,1)(-1,1).