题目内容
2.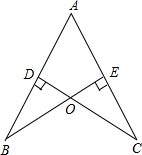 如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O.(1)求证:AD=AE;
(2)连接AO,证明:AO平分∠BAC.
分析 (1)根据AAS推出△ACD≌△ABE,根据全等三角形的性质得出即可;
(2)证Rt△ADO≌Rt△AEO,即可得出∠DAO=∠EAO,即OA平分∠DAE.
解答 解:(1)∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°,
在△ACD和△ABE中,
$\left\{\begin{array}{l}{∠ADC=∠AEB}\\{∠CAD=∠BAE}\\{AB=AC}\end{array}\right.$,
∴△ACD≌△ABE(AAS),
∴AD=AE;
(2)如图,连接OA,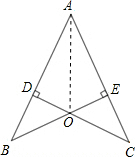
∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°.
在Rt△ADO和Rt△AEO中,
$\left\{\begin{array}{l}{OA=OA}\\{AD=AE}\end{array}\right.$,
∴Rt△ADO≌Rt△AEO(HL).
∴∠DAO=∠EAO,
∴OA平分∠DAE.
点评 本题考查了全等三角形的判定方法,以及全等三角形的对应边相等,对应角相等的性质,难度适中.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
13.甲看乙的方向为北偏东60°,那么乙看甲的方向是( )
| A. | 南偏东30° | B. | 南偏西30° | C. | 南偏东60° | D. | 南偏西60° |
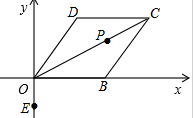 菱形ABCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,-1),则EP+BP的最小值是$\sqrt{5+2\sqrt{3}}$.
菱形ABCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,-1),则EP+BP的最小值是$\sqrt{5+2\sqrt{3}}$.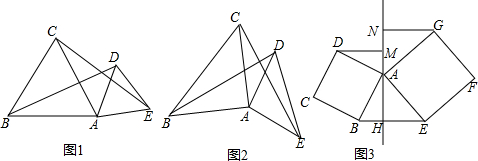
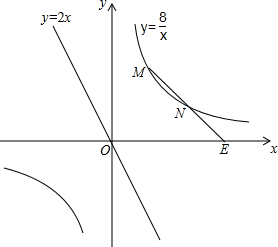 某数学兴趣小组的同学再一次探究中发现:若平面直角坐标系中有两点A(x1,y1)和B(x2,y2),则线段AB的中点C的坐标为($\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2}$).经过进一步的讨论,他们呢借助中位线和一次函数的知识证明了这一结论,请你使用该结论解答下面问题.
某数学兴趣小组的同学再一次探究中发现:若平面直角坐标系中有两点A(x1,y1)和B(x2,y2),则线段AB的中点C的坐标为($\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2}$).经过进一步的讨论,他们呢借助中位线和一次函数的知识证明了这一结论,请你使用该结论解答下面问题. 在长方形ABCD中,放入8个形状和大小都相同的长方形,位置与尺寸如图所示(单位:cm),则阴影部分的面积是112cm2.
在长方形ABCD中,放入8个形状和大小都相同的长方形,位置与尺寸如图所示(单位:cm),则阴影部分的面积是112cm2.