题目内容
15.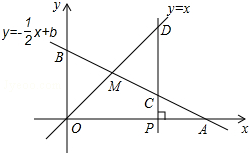 如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M(2,2),在x轴上有一动点P(a,0),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.
如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M(2,2),在x轴上有一动点P(a,0),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.(1)求点A的坐标;
(2)当a=-1时,求CD的长;
(3)当CD=2OB时,求a的值.
分析 (1)把M(2,2)代入y=-$\frac{1}{2}$x+b可计算出b=3,得到一次函数的解析式为y=-$\frac{1}{2}$x+3,然后根据x轴上点的坐标特征可确定A点坐标为(6,0);
(2)根据a=-1,则点P(-1,0),当x=-1时,y=-$\frac{1}{2}$x+3=-$\frac{1}{2}×$(-1)+3=$\frac{7}{2}$,确定点C的坐标为(-1,$\frac{7}{2}$),点D的坐标为(-1,-1),即可求出CD的长;
(3)再先确定B点坐标为(0,3),则OB=3,CD=2OB=6,再表示出C点坐标为(a,-$\frac{1}{2}$a+3),D点坐标为(a,a),所以|a-(-$\frac{1}{2}$a+3)|=6,然后解方程即可.
解答 解:(1)把M(2,2)代入y=-$\frac{1}{2}$x+b得:-$\frac{1}{2}$×2+b=2,
解得:b=3,
∴一次函数的解析式为y=-$\frac{1}{2}$x+3,
当y=0时,x=6,
∴A点坐标为(6,0);
(2)当a=-1时,则点P(-1,0),
当x=-1时,y=-$\frac{1}{2}$x+3=-$\frac{1}{2}×$(-1)+3=$\frac{7}{2}$,
则点C的坐标为(-1,$\frac{7}{2}$),点D的坐标为(-1,-1),
则CD=$\frac{7}{2}$-(-1)=$\frac{9}{2}$.
(3)把x=0代入y=-$\frac{1}{2}$x+3得y=3,
∴B点坐标为(0,3),
∵CD=2OB,
∴CD=6,
∵PC⊥x轴,
∴C点坐标为(a,-$\frac{1}{2}$a+3),D点坐标为(a,a)
∴|a-(-$\frac{1}{2}$a+3)|=6,
∴a=6或-2.
点评 本题考查了一次函数和两点之间的距离,解决本题的关键是求出点C和点D的坐标,根据两点之间的距离公式进行解决问题.

 阅读快车系列答案
阅读快车系列答案| A. | $\sqrt{{a}+1}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{10}$ |
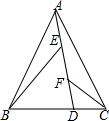 锐角三角形△ABC中,BA=AC,过点A的直线交BC边于点D,E、F是AD上两点,∠BEA=∠AFC且∠BEA与∠AFC都与∠BAC互补,猜想EF、BE、CF之间的关系并证明.
锐角三角形△ABC中,BA=AC,过点A的直线交BC边于点D,E、F是AD上两点,∠BEA=∠AFC且∠BEA与∠AFC都与∠BAC互补,猜想EF、BE、CF之间的关系并证明.