题目内容
19.寻找公式,求代数式的值:从2开始,连续的偶数相加,它们的和的情况如表:
(1)当n个最小的连续偶数相加时,它们的和S与n之间的关系,用公式表示S=n(n+1);
(2)按此规律计算:
(a)2+4+6+…+300的值;
(b)182+184+186+188+…+400的值.
分析 (1)找出结果中的因数与连续偶数个数之间的关系,就可解决问题;
(2)(a)直接利用(1)的结论,就可解决问题;
(b)只需把182+184+186+188+…+400转化为(2+4+6+8+…+400)-(2+4+6+8+…+180),然后运用(1)中的公式,就可解决问题.
解答 解:(1)S=2+4+6+8+…+2n=n(n+1).
故答案为n(n+1);
(2)(a)2+4+6+…+300=2+4+6+…+2×150=150×(150+1)=22650;
(b)182+184+186+188+…+400
=(2+4+6+8+…+400)-(2+4+6+8+…+180)
=200×201-90×91
=32010.
点评 本题是一道规律探究题,把首项不是2的连续偶数的和转化为首项是2的连续偶数的和,是解决第(2)(b)小题的关键.

练习册系列答案
相关题目
18.某次篮球联赛积分
(1)求胜一场、负一场积分各是多少?
(2)某队胜场总积分能等于它的负场总积分?
| 队名 | 比赛场次 | 胜场 | 负场 | 积分 |
| 前进 | 14 | 10 | 4 | 24 |
| 东方 | 10 | 4 | 4 | 24 |
| 光明 | 14 | 9 | 5 | 23 |
| 蓝天 | 14 | 9 | 5 | 23 |
| 雄鹰 | 14 | 7 | 7 | 21 |
| 远大 | 14 | 7 | 7 | 21 |
| 卫星 | 14 | 4 | 10 | 18 |
(2)某队胜场总积分能等于它的负场总积分?
8.下列四个条件,可以确定△ABC与△A′B′C′全等的是( )
| A. | BC=B′C′,AC=A′C′,∠B=∠B′ | B. | AB=AC,A′B′=A′C′,∠A=∠A′ | ||
| C. | AC=A′C′,∠A=∠A′,∠B=∠B′ | D. | ∠A=∠A′,∠B=∠B′,∠C=∠C′ |
 如图,O为直线AB上一点,∠AOC的平分线是OM,∠BOC的平分线是ON,求∠MON的度数.
如图,O为直线AB上一点,∠AOC的平分线是OM,∠BOC的平分线是ON,求∠MON的度数.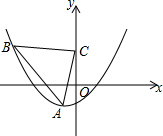 已知,抛物线y=$\frac{1}{8}$(x+1)2-2顶点为A,点B在抛物线上,以AB的斜边作等腰直角三角形,直角顶点C在y轴上,求C点坐标.
已知,抛物线y=$\frac{1}{8}$(x+1)2-2顶点为A,点B在抛物线上,以AB的斜边作等腰直角三角形,直角顶点C在y轴上,求C点坐标.