题目内容
2.有一列数a,b,c,d,…,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差.若第一个数a等于2,则第2014个数等于2.分析 首先根据条件求出前几个数,从中发现以下规律:每三个一循环,由2014=3×671+1可得第2014个数等于第一个数,问题得以解决.
解答 解:由题可得:
第一个数为2,
第二个数为1-$\frac{1}{2}$=$\frac{1}{2}$,
第三个数为1-$\frac{1}{\frac{1}{2}}$=1-2=-1,
第四个数为1-$\frac{1}{-1}$=2,
…
由此可得到:每三个一循环.
∵2014=3×671+1,
∴第2014个数等于第一个数,等于2.
故答案为2.
点评 本题是一道规律探究题,先算出前几个数,然后从中发现一般规律,是解决本题的关键.

练习册系列答案
相关题目
18.某次篮球联赛积分
(1)求胜一场、负一场积分各是多少?
(2)某队胜场总积分能等于它的负场总积分?
| 队名 | 比赛场次 | 胜场 | 负场 | 积分 |
| 前进 | 14 | 10 | 4 | 24 |
| 东方 | 10 | 4 | 4 | 24 |
| 光明 | 14 | 9 | 5 | 23 |
| 蓝天 | 14 | 9 | 5 | 23 |
| 雄鹰 | 14 | 7 | 7 | 21 |
| 远大 | 14 | 7 | 7 | 21 |
| 卫星 | 14 | 4 | 10 | 18 |
(2)某队胜场总积分能等于它的负场总积分?
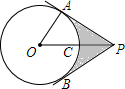 如图,PA,PB分别与⊙O相切于A,B两点,PO交⊙O于点C,PC=OC,AP=4$\sqrt{3}$cm.
如图,PA,PB分别与⊙O相切于A,B两点,PO交⊙O于点C,PC=OC,AP=4$\sqrt{3}$cm. 如图,∠BAC=30°,点P是∠BAC平分线上一点,PM∥AC交AB于点M,PD⊥AC于点D,若PD+PM=12,则AM=8.
如图,∠BAC=30°,点P是∠BAC平分线上一点,PM∥AC交AB于点M,PD⊥AC于点D,若PD+PM=12,则AM=8. 如图,O为直线AB上一点,∠AOC的平分线是OM,∠BOC的平分线是ON,求∠MON的度数.
如图,O为直线AB上一点,∠AOC的平分线是OM,∠BOC的平分线是ON,求∠MON的度数.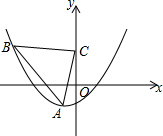 已知,抛物线y=$\frac{1}{8}$(x+1)2-2顶点为A,点B在抛物线上,以AB的斜边作等腰直角三角形,直角顶点C在y轴上,求C点坐标.
已知,抛物线y=$\frac{1}{8}$(x+1)2-2顶点为A,点B在抛物线上,以AB的斜边作等腰直角三角形,直角顶点C在y轴上,求C点坐标.