题目内容
11．
如图，将四边形纸片ABCD沿MN折叠，点A、D分别落在点A1、D1处．若∠1+∠2=140°，则∠B+∠C=110°．
分析 先根据∠1+∠2=40°得出∠AMN+∠DNM的度数，再由四边形内角和定理即可得出结论．
解答 解：∵∠1+∠2=40°，
∴∠AMN+∠DNM=$\frac{360°-140°}{2}$=110°．
∵∠A+∠D+（∠AMN+∠DNM）=360°，∠A+∠D+（∠B+∠C）=360°，
∴∠B+∠C=∠AMN+∠DNM=110°．
故答案为：110．
点评 本题考查的是翻折变换，熟知图形翻折不变性的性质是解答此题的关键．
练习册系列答案
相关题目
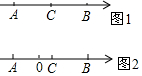如图1，在数轴上，A点、B点与C点的距离相等．
观察图，先填空，然后回答问题：
如图，已知点A，D，B在同一直线上，∠1=∠2，∠3=∠E，若∠DAE=100°，∠E=30°，求∠B的度数．
如图是某种蜡烛在燃烧过程中高度与时间之间关系的图象，由图象解答下列问题：