题目内容
13．
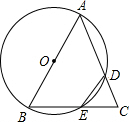如图，已知等边△ABC的边长为6，以AB为直径的⊙O与边AC、BC分别交于D、E两点，则劣弧$\widehat{DE}$的长为π．
分析 连接OD、OE，先证明△AOD、△BOE是等边三角形，得出∠AOD=∠BOE=60°，求出∠DOE=60°，再由弧长公式即可得出答案．
解答 解：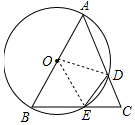
连接OD、OE，如图所示：
∵△ABC是等边三角形，
∴∠A=∠B=∠C=60°，
∵OA=OD，OB=OE，
∴△AOD、△BOE是等边三角形，
∴∠AOD=∠BOE=60°，
∴∠DOE=60°，
∵OA=$\frac{1}{2}$AB=3，
∴$\widehat{DE}$的长=$\frac{60π×3}{180}$=π；
故答案为：π．
点评 本题考查了等边三角形的性质与判定、弧长公式；熟练掌握弧长公式，证明三角形是等边三角形是解决问题的关键．
练习册系列答案
导学全程练创优训练系列答案
相关题目
3．某种计算机完成一次基本运算的时间约为0.000000005s，把0.000000005s用科学记数法可以表示为（ ）
| A． | 0.5×10-8s | B． | 5×10-9s | C． | 5×10-8s | D． | 0.5×10-9s |
1．
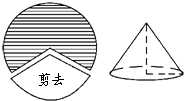如图，将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形，用剩下的扇形围成一个圆锥的侧面（接缝忽略不计），这个圆锥的高是（ ）
如图，将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形，用剩下的扇形围成一个圆锥的侧面（接缝忽略不计），这个圆锥的高是（ ）| A． | 12cm | B． | 8cm | C． | 20cm | D． | 18cm |
8．
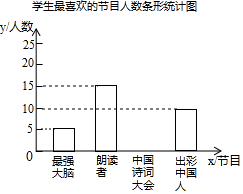为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随机抽取了x名学生进行调查统计（要求每名学生选出并且只能选出一个自己最喜爱的节目），并将调查结果绘制成如图统计图表：
学生最喜爱的节目人数统计表
根据以上提供的信息，解答下列问题：
（1）x=50，a=20，b=30；
（2）补全上面的条形统计图；
（3）若该校共有学生1000名，根据抽样调查结果，估计该校最喜爱《中国诗词大会》节目的学生有多少名．
为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随机抽取了x名学生进行调查统计（要求每名学生选出并且只能选出一个自己最喜爱的节目），并将调查结果绘制成如图统计图表：学生最喜爱的节目人数统计表
| 节目 | 人数（名） | 百分比 |
| 最强大脑 | 5 | 10% |
| 朗读者 | 15 | b% |
| 中国诗词大会 | a | 40% |
| 出彩中国人 | 10 | 20% |
（1）x=50，a=20，b=30；
（2）补全上面的条形统计图；
（3）若该校共有学生1000名，根据抽样调查结果，估计该校最喜爱《中国诗词大会》节目的学生有多少名．
18．若二元一次方程组$\left\{\begin{array}{l}x+y=3\\ 3x-5y=4\end{array}\right.$的解为$\left\{\begin{array}{l}x=a\\ y=b\end{array}\right.$，则a-b=（ ）
| A． | 1 | B． | 3 | C． | $-\frac{1}{4}$ | D． | $\frac{7}{4}$ |
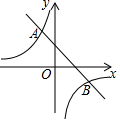如图，一次函数y=k1x+b（k1≠0）与反比例函数y=$\frac{k_2}{x}$（k2≠0）的图象交于点A（-1，2），B（m，-1）．