题目内容
如图,某学校旗杆AB旁边有一个半侧的时钟模型,时钟的9点和3点的刻度线刚好和地面重合,半圆的半径2m,旗杆的底端A到钟面9点刻度C的距离为11m,一天小明观察到阳光下旗杆顶端B的影子刚好投到时钟的11点的刻度上,同时测得1米长的标杆的影长1.2m.求旗杆AB的高度.


考点:相似三角形的应用,解直角三角形的应用
专题:
分析:设半圆圆心为O,连接OD、CD,可得△OCD是等边三角形,过点D作DE⊥OC于E,作DF⊥AB于F,可得四边形AEDF是矩形,然后求出DE的长度,根据同时同地物高与影长成正比求出BF,然后根据AB=BF+AF计算即可得解.
解答: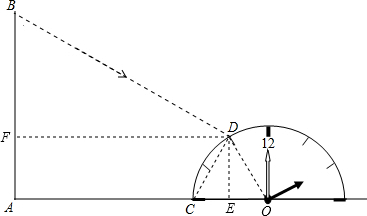 解:如图,设半圆圆心为O,连接OD、CD,
解:如图,设半圆圆心为O,连接OD、CD,
∵点D在11点的刻度上,
∴∠COD=60°,
∴△OCD是等边三角形,
过点D作DE⊥OC于E,作DF⊥AB于F,则四边形AEDF是矩形,
∵半圆的半径2m,
∴DE=2×
=
,
同时测得1米长的标杆的影长1.2m,
∴
=
,
解得BF=10,
所以AB=BF+AF=(10+
)m.
答:旗杆AB的高度(10+
)m.
 解:如图,设半圆圆心为O,连接OD、CD,
解:如图,设半圆圆心为O,连接OD、CD,∵点D在11点的刻度上,
∴∠COD=60°,
∴△OCD是等边三角形,
过点D作DE⊥OC于E,作DF⊥AB于F,则四边形AEDF是矩形,
∵半圆的半径2m,
∴DE=2×
| ||
| 2 |
| 3 |
同时测得1米长的标杆的影长1.2m,
∴
| BF |
| 12 |
| 1 |
| 1.2 |
解得BF=10,
所以AB=BF+AF=(10+
| 3 |
答:旗杆AB的高度(10+
| 3 |
点评:本题考查了相似三角形的应用,主要利用了同时同地物高与影长成正比,等边三角形的判定与性质,作辅助线构造出直角三角形和矩形是解题的关键.

练习册系列答案
相关题目
 如图,正比例函数y=x与反比例函数y=
如图,正比例函数y=x与反比例函数y=
 如图,A、B是双曲线y=
如图,A、B是双曲线y=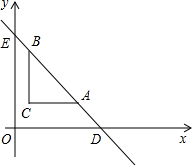 如图,在平面直角坐标系中,过点C(1,2)分别作x轴、y轴的平行线,交直线DE于A、B两点,点D的坐标是(6,0),点E的坐标是(0,6).
如图,在平面直角坐标系中,过点C(1,2)分别作x轴、y轴的平行线,交直线DE于A、B两点,点D的坐标是(6,0),点E的坐标是(0,6).