题目内容
已知关于x的一元二次方程:x2-(2k+1)+4(k-
)=0.
(1)求证:这个方程总有两个实数根;
(2)若等腰△ABC的一边长a=4,另两边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
| 1 |
| 2 |
(1)求证:这个方程总有两个实数根;
(2)若等腰△ABC的一边长a=4,另两边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
考点:根的判别式,三角形三边关系,等腰三角形的性质
专题:
分析:(1)先计算△,化简得到△=(2k-3)2,易得△≥0,然后根据△的意义即可得到结论;
(2)利用求根公式计算出方程的两根x1=2k-1,x2=2,则可设b=2k-1,c=2,然后讨论:当a、b为腰;当b、c为腰,分别求出边长,但要满足三角形三边的关系,最后计算周长.
(2)利用求根公式计算出方程的两根x1=2k-1,x2=2,则可设b=2k-1,c=2,然后讨论:当a、b为腰;当b、c为腰,分别求出边长,但要满足三角形三边的关系,最后计算周长.
解答:(1)证明:△=(2k+1)2-4×1×4(k-
)
=4k2-12k+9
=(2k-3)2,
∵无论k取什么实数值,(2k-3)2≥0,
∴△≥0,
∴无论k取什么实数值,方程总有实数根;
(2)解:∵x=
,
∴x1=2k-1,x2=2,
∵b,c恰好是这个方程的两个实数根,设b=2k-1,c=2,
当a、b为腰,则a=b=4,即2k-1=4,解得k=
,此时三角形的周长=4+4+2=10;
当b、c为腰时,b=c=2,此时b+c=a,故此种情况不存在.
综上所述,△ABC的周长为10.
| 1 |
| 2 |
=4k2-12k+9
=(2k-3)2,
∵无论k取什么实数值,(2k-3)2≥0,
∴△≥0,
∴无论k取什么实数值,方程总有实数根;
(2)解:∵x=
| 2k+1±(2k-3) |
| 2 |
∴x1=2k-1,x2=2,
∵b,c恰好是这个方程的两个实数根,设b=2k-1,c=2,
当a、b为腰,则a=b=4,即2k-1=4,解得k=
| 5 |
| 2 |
当b、c为腰时,b=c=2,此时b+c=a,故此种情况不存在.
综上所述,△ABC的周长为10.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了三角形三边的关系以及分类讨论思想的运用.

练习册系列答案
相关题目
下列命题中错误的是( )
| A、平行四边形的对角线互相平分 |
| B、等腰梯形的对角线互相平分 |
| C、菱形的对角线互相平分 |
| D、正方形的对角线互相平分 |
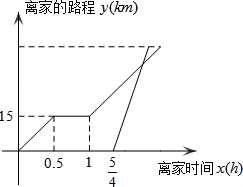 周末,小明骑电动车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时15分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的2倍.
周末,小明骑电动车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时15分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的2倍.
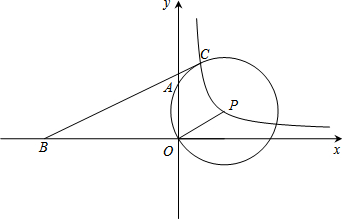 如图,在平面直角坐标系中,⊙P过原点O和y轴上的点A,点C(1,3)也在⊙P上,A、B两点的坐标分别为(0,2)和(-5,0),点P(2,a)在反比例函数y=
如图,在平面直角坐标系中,⊙P过原点O和y轴上的点A,点C(1,3)也在⊙P上,A、B两点的坐标分别为(0,2)和(-5,0),点P(2,a)在反比例函数y=