题目内容
 如图,A、B是双曲线y=
如图,A、B是双曲线y=| k |
| x |
(1)求k的值;
(2)求△OAC的面积.
考点:反比例函数系数k的几何意义,反比例函数图象上点的坐标特征
专题:
分析:(1)把点A(1,4)代入y=
,即可求出k的值;
(2)作AD⊥x轴于点D,BE⊥x轴于点E,由A的坐标是(1,4),得到AD=4,OD=1,根据B为AC的中点,求出B点坐标为(2,2),则DE=CE=2-1=1,即OC=3,然后根据三角形面积公式即可求解.
| k |
| x |
(2)作AD⊥x轴于点D,BE⊥x轴于点E,由A的坐标是(1,4),得到AD=4,OD=1,根据B为AC的中点,求出B点坐标为(2,2),则DE=CE=2-1=1,即OC=3,然后根据三角形面积公式即可求解.
解答: 解:(1)∵A是双曲线y=
解:(1)∵A是双曲线y=
上的点,点A的坐标是(1,4),
∴把x=1,y=4代入y=
,得k=1×4=4;
(2)作AD⊥x轴于点D,BE⊥x轴于点E,
∵A(1,4),
∴AD=4,OD=1.
又∵B为AC的中点,
∴BE=
AD=2,且CE=DE,
∴B点的纵坐标为2,则有B点坐标为(2,2).
∴DE=CE=2-1=1,即OC=3,
∴S△OAC=
•AD•OC=
×4×3=6.
 解:(1)∵A是双曲线y=
解:(1)∵A是双曲线y=| k |
| x |
∴把x=1,y=4代入y=
| k |
| x |
(2)作AD⊥x轴于点D,BE⊥x轴于点E,
∵A(1,4),
∴AD=4,OD=1.
又∵B为AC的中点,
∴BE=
| 1 |
| 2 |
∴B点的纵坐标为2,则有B点坐标为(2,2).
∴DE=CE=2-1=1,即OC=3,
∴S△OAC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了反比例函数图象上点的坐标特征,三角形的面积,难度适中.准确作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
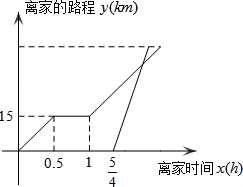 周末,小明骑电动车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时15分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的2倍.
周末,小明骑电动车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时15分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的2倍.
 为鼓励教师爱岗敬业,某市开展了“我最喜爱的老师”评选活动.某中学确定如下评选方案:由学生和教师代表对4名候选教师进行投票,每票只能选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总得票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
为鼓励教师爱岗敬业,某市开展了“我最喜爱的老师”评选活动.某中学确定如下评选方案:由学生和教师代表对4名候选教师进行投票,每票只能选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总得票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).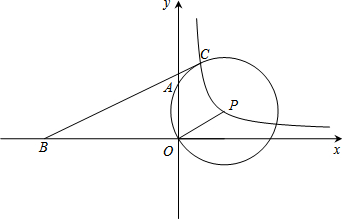 如图,在平面直角坐标系中,⊙P过原点O和y轴上的点A,点C(1,3)也在⊙P上,A、B两点的坐标分别为(0,2)和(-5,0),点P(2,a)在反比例函数y=
如图,在平面直角坐标系中,⊙P过原点O和y轴上的点A,点C(1,3)也在⊙P上,A、B两点的坐标分别为(0,2)和(-5,0),点P(2,a)在反比例函数y=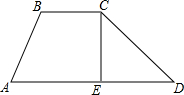 如图,水库大坝的横断面近似于梯形ABCD,迎水坡BC的倾斜角∠D=30°,背水坡AB的坡比为1.2:1,坝顶BC=6米,坝高CE=8米,求CD和AD的长.
如图,水库大坝的横断面近似于梯形ABCD,迎水坡BC的倾斜角∠D=30°,背水坡AB的坡比为1.2:1,坝顶BC=6米,坝高CE=8米,求CD和AD的长.