Question

15．问题探究：三角形的内接四边形指顶点在三角形各边上的四边形．
（1）如图1，△ABC中，AB=AC，正方形MNEF的顶点M、E在BC上，顶点N在AB上，请以点B为位似中心，作△ABC的内接正方形．（不写作法）．
（2）如图2，△ABC中，BC=12，∠B=45°，AD⊥BC于点D，AD=8，请以点D为位似中心，作△ABC的内接正方形，并求出所作正方形的面积（不写作法）．
问题解决
（3）如图3，将（2）中的△ABC翻折得到四边形ABEC，对角线AE、BC相交于点D，请以点D为位似中心作正方形MNPQ，使得点M、N、P、Q在正方形ABEC的各边上．
要求：①写出作法，证明四边形MNPQ是正方形；
②求出正方形MNPQ的面积．

Answer 1

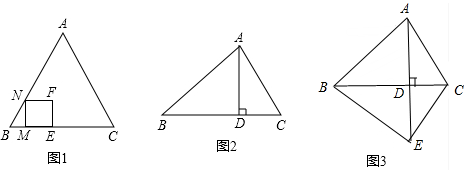
分析 （1）如图1中，延长BF交AC于F′，作F′E′∥EF交BC于E′，作F′N′∥BC交AB于N′，作N′M′∥EF交BC于M′，正方形M′N′F′E′即为所求．
（2）如图2中，正方形MNEF的顶点M、F在BC上，且DM=2DF．延长DE交AC于E′，作E′F′⊥BC于F′，延长DN交AB于N′，作N′M′⊥BC于M′，正方形M′N′E′F′即为所求．设正方形M′N′E′F′的边长为x，由N′E′∥BC，推出△AN′E′∽△ABC，可得$\frac{x}{12}$=$\frac{8-x}{8}$，解方程即可．
（3）作正方形MNEF，使得MN∥AD，MN交BC于P，EF交BC于Q，且PN=PM，PD=2DQ，延长DE交AC于E′，延长DN交AB于N′，延长DM交BE于M′，延长DF交EC于F′，连接M′N′，N′E′，E′F′，F′M′，则四边形M′N′E′F′即为所求．设E′F′交BC于G，M′N′交BC于H．首先证明四边形M′N′E′F′是平行四边形，再证明有一个角是直角，邻边相等即可．

解答 解：（1）如图1中，请以点B为位似中心，△ABC的内接正方形M′N′F′E′如图所示．

（2）如图2中，以点D为位似中心，△ABC的内接正方形M′N′E′F′如图所示．

正方形MNEF的顶点M、F在BC上，且DM=2DF．延长DE交AC于E′，作E′F′⊥BC于F′，延长DN交AB于N′，作N′M′⊥BC于M′，正方形M′N′E′F′即为所求．
设正方形M′N′E′F′的边长为x，
∵N′E′∥BC，
∴△AN′E′∽△ABC，
∴$\frac{x}{12}$=$\frac{8-x}{8}$，
∴x=$\frac{24}{5}$，
∴正方形M′N′E′F′的边长为$\frac{24}{5}$．

（3）如图3中，

作正方形MNEF，使得MN∥AD，MN交BC于P，EF交BC于Q，且PN=PM，PD=2DQ，延长DE交AC于E′，延长DN交AB于N′，延长DM交BE于M′，延长DF交EC于F′，连接M′N′，N′E′，E′F′，F′M′，则四边形M′N′E′F′即为所求．设E′F′交BC于G，M′N′交BC于H．
由题意AB=AD=8，DC=4，
∴AD=2DC，
∵△BCE是由△ABC翻折得到，PN=PM，QE=QF，
∴根据对称性可知，E′F′∥AE∥M′N′，
∵EQ：DQ=3：2，
∴E′G：DG=3：2，
∵E′G：GC=AD：DC=2：1，
∴AE′：E′C=DG：GC=4：3，同理可证AN′：BN′=4：3，
∴AN′：BN′=AE′：E′C，
∴E′N′∥BC，同理可证M′F′∥BC，
∴四边形M′N′E′F′是平行四边形，易知∠M′N′E′=90°，
∴四边形M′N′E′F′是矩形，
∵EN∥E′N′，EF∥E′F′，
∴EN：E′N′=DE：DE′=EF：E′F′，
∵EN=EF，
∴N′E′=E′F′，
∴四边形M′N′E′F′是正方形．设边长为a，
∵N′E′∥BC，
∴△AN′E′∽△ABC，
∴$\frac{a}{12}$=$\frac{8-\frac{1}{2}a}{8}$，
∴a=$\frac{48}{7}$
∴正方形M′N′E′F′的边长为$\frac{48}{7}$．

点评 本题考查四边形综合题、位似变换、相似三角形的判定和性质、正方形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会利用位似变换构建正方形，学会用方程的思想思考问题，把问题转化为方程解决，属于中考压轴题．