题目内容
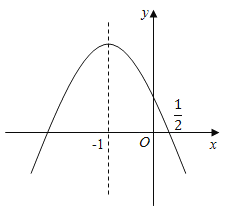
【题目】已知二次函数
的图象如图所示．下列结论：①
；②
；③
；④
其中正确的个数有（ ）
A.
B.
C.
D.
【答案】D
【解析】
由抛物线开口方向得a＜0，由抛物线对称轴在y轴的左侧得a、b同号，即b＜0，由抛物线与y轴的交点在x轴上方得c＞0，所以abc＞0；根据抛物线对称轴的位置得到1＜
＜0，则根据不等式性质即可得到2ab＜0；由于x＝2时，对应的函数值小于0，则4a2b＋c＜0；同样当x＝1时，ab＋c＞0，x＝1时，a＋b＋c＜0，则（ab＋c）（a＋b＋c）＜0，利用平方差公式展开得到（a＋c）2b2＜0，即（a＋c）2＜b2．
∵抛物线开口向下，
∴a＜0，
∵抛物线的对称轴在y轴的左侧，
∴x＝＜0，
∴b＜0，
∵抛物线与y轴的交点在x轴上方，
∴c＞0，
∴abc＞0，（故①正确）；
∵1＜＜0，
∴2a＞b，
∴2ab＜0，（故②错误）；
∵当x＝2时，y＜0，
∴4a2b＋c＜0，（故③错误）；
∵当x＝1时，y＞0，
∴ab＋c＞0，
∵当x＝1时，y＜0，
∴a＋b＋c＜0，
∴（ab＋c）（a＋b＋c）＜0，即（a＋cb）（a＋c＋b）＜0，
∴（a＋c）2b2＜0，（故④错误）．
综上所述，正确的个数有1个；
故选：D．
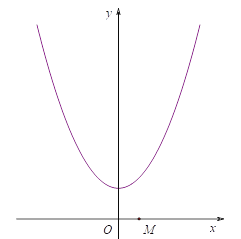
【题目】已知函数
，
，探究函数图象和性质过程如下：
（1）下表是y与x的几组值，则解析式中的m＝ ，表格中的n＝ ;
x | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y |
|
|
| 1 |
| 3 |
| 4 |
| 3 | n | 0 | … |
（2）在平面直角坐标系中描出表格中各点，并画出函数图象：
（3）若A（x1，y1）、B（x2，y2）、C（x3，y3）为函数图象上的三个点，其中x2+x3＞4且﹣1＜x1＜0＜x2＜2＜x3＜4，则y1、y2、y3之间的大小关系是 ；
（4）若直线y＝k+1与该函数图象有且仅有一个交点，则k的取值范围为 ．
