Question

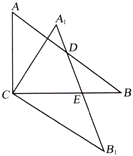
【题目】如图，AB是⊙C的直径，M、D两点在AB的延长线上，E是⊙C的点，且DE2＝DBDA，延长AE至F，使得AE＝EF，设BF＝5，cos∠BED＝．

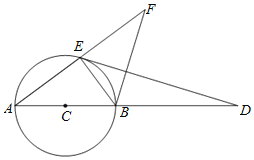
（1）求证：△DEB∽△DAE；

（2）求DA、DE的长；

（3）若点F在B、E、M三点确定的圆上，求MD的长．

Answer 1

【答案】（1）见解析；（2）AD＝，ED＝；（3）

【解析】

（1）利用两边成比例夹角相等两三角形相似证明即可．

（2）由 ，即： ，即可求解．

（3）在△BED中，过点B作HB⊥ED于点H，设HD＝x，利用勾股定理构建方程解决问题即可．

解：（1）∵DE2＝DBDA，

∴ ，

又∵∠D＝∠D，

∴△DEB∽△DAE．

（2）∵△DEB∽△DAE，

∴∠DEB＝∠DAE＝α，

∵AB是直径，

∴∠AEB＝90°，又AE＝EF，

∴AB＝BF＝5，

∴∠BFE＝∠BAE＝α，则BF⊥ED交于点H，

∵ ，则BE＝3，AE＝4

∴，即：

解得：

则AD＝AB+BD＝，

ED＝．

（3）由点F在B、E、M三点确定的圆上，则BF是该圆的直径，连接MF，

∵BF⊥ED，∠BMF＝90°，∴∠MFB＝∠D＝β，

在△BED中，过点B作HB⊥ED于点H，

设HD＝x，则

则

解得：

则 ，则

DM＝BD﹣MB＝．