题目内容
直线l1：y=k1x+b与直线l2：y=k2x在同一平面直角坐标系中的图象如图，则关于x的不等式k2x＞k1x+b的解集为（ ）| A、x＜-1 | B、x＞1 |
| C、x＜3 | D、x＞3 |
考点：一次函数与一元一次不等式
专题：数形结合
分析：观察函数图象得到当x＜-1时，直线y=k2x都在直线y=k1x+b的上方，即有k2x＞k1x+b．
解答：解：当x＜-1时，k2x＞k1x+b．
故选A．
故选A．
点评：本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数y=ax+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
将一组数1，2，3…10，按下列顺序排列：
1，2，3，4，5；
6，7，8，9，10．
若4的位置记作（1，4），8的位置记作（2，3），则这组数中10的位置记作（ ）
1，2，3，4，5；
6，7，8，9，10．
若4的位置记作（1，4），8的位置记作（2，3），则这组数中10的位置记作（ ）
| A、（5，10） |
| B、（2，5） |
| C、（1，5） |
| D、（6，10） |
如图各曲线中，不表示y是x的函数的是（ ）
A、 |
B、 |
C、 |
D、 |
如图，矩形ABCD中，AB=8cm，AD=12cm，AC与BD交于点O，M是BC的中点．P、Q两点沿着B→C→D方向分别从点B、点M同时出发，并都以1cm/s的速度运动，当点Q到达D点时，两点同时停止运动．在P、Q两点运动的过程中，与△OPQ的面积随时间t变化的图象最接近的是（ ）
下列命题中的假命题是（ ）
| A、互余两角的和是90° |
| B、多边形的外角和为360° |
| C、若a＞b，则a2＞b2 |
| D、两直线平行，同旁内角互补 |
某电梯标明“载客不超过13人”，若载客人数为x，x为自然数，则“载客不超过13人”用不等式表示为（ ）
| A、x＜13 | B、x＞13 |
| C、x≤13 | D、x≥13 |
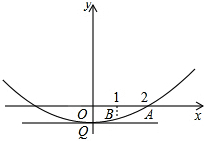如图，在平面直角坐标系中，已知二次函数