题目内容
 如图,矩形ABCD中,AB=8cm,AD=12cm,AC与BD交于点O,M是BC的中点.P、Q两点沿着B→C→D方向分别从点B、点M同时出发,并都以1cm/s的速度运动,当点Q到达D点时,两点同时停止运动.在P、Q两点运动的过程中,与△OPQ的面积随时间t变化的图象最接近的是( )
如图,矩形ABCD中,AB=8cm,AD=12cm,AC与BD交于点O,M是BC的中点.P、Q两点沿着B→C→D方向分别从点B、点M同时出发,并都以1cm/s的速度运动,当点Q到达D点时,两点同时停止运动.在P、Q两点运动的过程中,与△OPQ的面积随时间t变化的图象最接近的是( )A、 |
B、 |
C、 |
D、 |
考点:动点问题的函数图象
专题:
分析:根据矩形的性质求出点O到BC的距离等于4,到CD的距离等于6,求出点Q到达点C的时间为6秒,点P到达点C的时间为12秒,点Q到达点D的时间为14秒,然后分①0≤t≤6时,点P、Q都在BC上,表示出PQ,然后根据三角形的面积公式列式计算即可;②6<t≤12时,点P在BC上,点Q在CD上,表示出CP、CQ,然后根据S△OPQ=S△COP+S△COQ-S△PCQ列式整理即可得解;③12<t≤14时,表示出PQ,然后根据三角形的面积公式列式计算即可得解.
解答:解:∵矩形ABCD中,AB=8cm,AD=12cm,AC与BD交于点O,
∴点O到BC的距离=
AB=4,到CD的距离=
AD=6,
∵点M是BC的中点,
∴CM=
BC=6,
∴点Q到达点C的时间为6÷1=6秒,
点P到达点C的时间为12÷1=12秒,
点Q到达点D的时间为(6+8)÷1=14秒,
①0≤t≤6时,点P、Q都在BC上,PQ=6,
△OPQ的面积=
×6×4=12;
②6<t≤12时,点P在BC上,点Q在CD上,
CP=12-t,CQ=t-6,
S△OPQ=S△COP+S△COQ-S△PCQ,
=
×(12-t)×4+
×(t-6)×6-
×(12-t)×(t-6),
=
t2-8t+42,
=
(t-8)2+10,
③12<t≤14时,PQ=6,
△OPQ的面积=
×6×6=18;
纵观各选项,只有B选项图形符合.
故选B.
∴点O到BC的距离=
| 1 |
| 2 |
| 1 |
| 2 |
∵点M是BC的中点,
∴CM=
| 1 |
| 2 |
∴点Q到达点C的时间为6÷1=6秒,
点P到达点C的时间为12÷1=12秒,
点Q到达点D的时间为(6+8)÷1=14秒,
①0≤t≤6时,点P、Q都在BC上,PQ=6,
△OPQ的面积=
| 1 |
| 2 |
②6<t≤12时,点P在BC上,点Q在CD上,
CP=12-t,CQ=t-6,
S△OPQ=S△COP+S△COQ-S△PCQ,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
③12<t≤14时,PQ=6,
△OPQ的面积=
| 1 |
| 2 |
纵观各选项,只有B选项图形符合.
故选B.
点评:本题考查了动点问题函数图象,主要利用了矩形的性质,三角形的面积,求出点P、Q到达各转折点时的时间,然后分情况讨论是解题的关键,点P在BC上,点Q在CD上时三角形的面积表示是本题的难点.

练习册系列答案
相关题目
下列分解因式正确的是( )
| A、3x2-6x=x(3x-6) |
| B、a2-b2=(a+b)(a-b) |
| C、4x2-y2=(4x+y)(4x-y) |
| D、4x2-2xy+y2=(2x-y)2 |
实数
的值等于( )
| 16 |
| A、±4 | B、±2 | C、4 | D、2 |
计算x5•x5的值为( )
| A、x5 |
| B、x10 |
| C、x25 |
| D、2x5 |
2013年1月9日,全国中东部地区陷入严重的雾霾和污染天气中,13日10时北京甚至发布了北京气象史上首个霾橙色预警.从东北到西北,从华北到中部导致黄淮、江南地区,都出现了大范围的重度和严重污染,PM2.5是形成雾霾天气的罪魁祸首,PM2.5是指大气中直径≤2.5微米的颗粒物.也称为可入肺颗粒物,已知1微米是0.000001米,2.5微米是( )米.
| A、2.5×10-5 |
| B、25×10-4 |
| C、2.5×10-6 |
| D、2.5×106 |
不等式2x+3≥5的解集在数轴上表示为( )
A、 |
B、 |
C、 |
D、 |
 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图,则关于x的不等式k2x>k1x+b的解集为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图,则关于x的不等式k2x>k1x+b的解集为( )| A、x<-1 | B、x>1 |
| C、x<3 | D、x>3 |
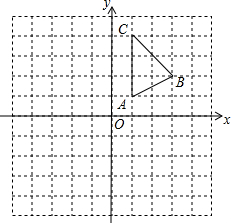 在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,1),B(3,2),C(1,4).
在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,1),B(3,2),C(1,4).