题目内容
4.(1)解不等式组$\left\{\begin{array}{l}{x+3>0}\\{2(x-1)+3≥3x}\end{array}\right.$,并判断x=$\sqrt{3}$是否为该不等式组的解.(2)先化简,再求值:($\frac{1}{a+1}$+1)÷$\frac{{a}^{2}-4}{a+1}$,其中a=-3.
分析 (1)分别求出不等式组中两不等式的解集,找出两解集的公共部分确定出不等式组的解集,即可作出判断;
(2)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把a的值代入计算即可求出值.
解答 解:(1)$\left\{\begin{array}{l}{x+3>0①}\\{2(x-1)+3>3x②}\end{array}\right.$,
由①得:x>-3;
由②得:x<1,
∴不等式组的解集为-3<x<1,
则x=$\sqrt{3}$不是该不等式组的解;
(2)原式=$\frac{a+2}{a+1}$•$\frac{a+1}{(a+2)(a-2)}$=$\frac{1}{a-2}$,
当a=-3时,原式=-$\frac{1}{5}$.
点评 此题考查了分式的化简求值,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.一次函数y=kx+b的图象与x轴、y轴的交点坐标分别是(-2,0),(0,-1),这个一次函数的解析式为( )
| A. | y=$\frac{1}{2}$x-1 | B. | y=2x+2 | C. | y=-x-1 | D. | y=2x-1 |
 解不等式组$\left\{\begin{array}{l}{4(x+1)<7x+10}\\{3-x≥\frac{x+9}{5}}\end{array}\right.$把它的解集在数轴上表示出来,并判断-1这个数是否为该不等式组的解.
解不等式组$\left\{\begin{array}{l}{4(x+1)<7x+10}\\{3-x≥\frac{x+9}{5}}\end{array}\right.$把它的解集在数轴上表示出来,并判断-1这个数是否为该不等式组的解.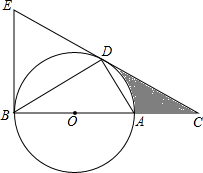 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
 如图,过矩形ABCD的顶点B作BE∥AC,垂足为E,延长BE交AD于F,若点F是边AD的中点,则sin∠ACD的值是$\frac{\sqrt{6}}{3}$.
如图,过矩形ABCD的顶点B作BE∥AC,垂足为E,延长BE交AD于F,若点F是边AD的中点,则sin∠ACD的值是$\frac{\sqrt{6}}{3}$.