��Ŀ����
12���Ķ���֤�������Ķ����²��ϣ��������Ӧ������������������ϲ��ϣ�֤�����½��ۣ�
��˵��ϣ���ϴ����˹��Pythagonas��Լ��Ԫ570��-Լ��Ԫǰ500�꣩ѧ�ɵ���ѧ�Ҿ�����ɳ̲���о���ѧ���⣮������ɳ̲�ϻ������Сʯ������ʾ�������磬�����о���1��3��6��10��������Щ��������ͼ����ʾ�������ε����ʾ�����Ǿͽ����Ϊ������������n����������������$\frac{n��n+1��}{2}$��n��1����ʾ��
������������ϲ��ϣ�֤�����½��ۣ�

��1������һ������������8�ټ�1��һ����ȫƽ������
��2�������������������ĺ���һ����ȫƽ������
���� ��1����n����������$\frac{n��n+1��}{2}$��8�ټ�1����������ȫƽ����ʽ�����ó��𰸼��ɣ�
��2���ֱ���n��ʾ����n��n+1��������������һ����������ó��𰸼��ɣ�
��� ֤������1����$\frac{n��n+1��}{2}$��8+1=4n2+4n+1=��2n+1��2��
������һ������������8�ټ�1��һ����ȫƽ������
��2���ߵ�n����������Ϊ$\frac{n��n+1��}{2}$����n+1����������Ϊ$\frac{��n+1����n+2��}{2}$��
�����������������ĺ�Ϊ��$\frac{n��n+1��}{2}$+$\frac{��n+1����n+2��}{2}$=$\frac{��n+1����2n+2��}{2}$=��n+1��2��
�������������������ĺ���һ����ȫƽ������
���� ���⿼��ͼ�������ֵı仯���ɼ���ȫƽ����������ĸ��ʾ����n������������������ȫƽ����ʽ��ʽ�ֽ��ǽ������Ĺؼ���

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
10�����и�ʽ������ȷ���ǣ�������
| A�� | a3•a=a4 | B�� | 2a3+a3=3a6 | C�� | ��-a2b��3=a6b3 | D�� | ��b+2a����2a-b��=b2-4a2 |
2��Ҫʹ��ʽ$\frac{-5}{x-1}$�����壬��x��ȡֵ��Χ�ǣ�������
| A�� | x��1 | B�� | x��1 | C�� | x��1 | D�� | x��-1 |
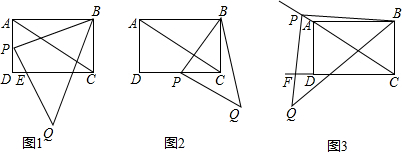
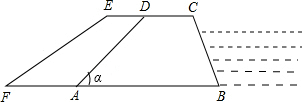 ��ͼ��ij�̰ӵĺ����������ABCD����ˮ��AD���¶ȣ���tan����Ϊ1��1.2���Ӹ�10�ף�Ϊ����߰ӵķ�������������ز��ž����ӹ̵̰ӣ�Ҫ�Ӷ�CD�ӿ�2�ף��γ��µı�ˮ��EF�����¶�Ϊ1��1.4����֪�̰��ܳ���Ϊ1000�ף�
��ͼ��ij�̰ӵĺ����������ABCD����ˮ��AD���¶ȣ���tan����Ϊ1��1.2���Ӹ�10�ף�Ϊ����߰ӵķ�������������ز��ž����ӹ̵̰ӣ�Ҫ�Ӷ�CD�ӿ�2�ף��γ��µı�ˮ��EF�����¶�Ϊ1��1.4����֪�̰��ܳ���Ϊ1000�ף�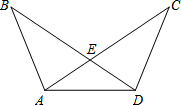 ��֪����ͼ����B=��C��AB=DC����֤����EAD=��EDA��
��֪����ͼ����B=��C��AB=DC����֤����EAD=��EDA��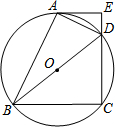 ��ͼ���ı���ABCD �ڽ��ڡ�O��BD�ǡ�O��ֱ��������A����O������AE��CD���ӳ����ڵ�E��DAƽ�֡�BDE��
��ͼ���ı���ABCD �ڽ��ڡ�O��BD�ǡ�O��ֱ��������A����O������AE��CD���ӳ����ڵ�E��DAƽ�֡�BDE��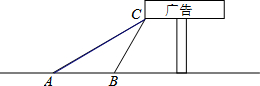 ��ͼ��ijѧУ��ѧ��ȤС�����˽⡰��25�����缼�ɽ���������ʱ������Ƶĸ߶ȣ�������A�㴦��ù���Ƶ�C�������Ϊ30�㣬Ȼ��������ǰ��10m�����B�����ֲ��C�������Ϊ60�㣮��������������������Ƶ�C�������ĸ߶ȣ�������������ţ�
��ͼ��ijѧУ��ѧ��ȤС�����˽⡰��25�����缼�ɽ���������ʱ������Ƶĸ߶ȣ�������A�㴦��ù���Ƶ�C�������Ϊ30�㣬Ȼ��������ǰ��10m�����B�����ֲ��C�������Ϊ60�㣮��������������������Ƶ�C�������ĸ߶ȣ�������������ţ�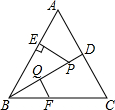 ��ͼ����ABC�ǵȱ������Σ�P�ǡ�ABC��ƽ����BD��һ�㣬PE��AB�ڵ�E���߶�BP�Ĵ�ֱƽ���߽�BC�ڵ�F������Ϊ��Q�����BF=a����ôPE=$\frac{\sqrt{3}}{2}$a���ú�a�Ĵ���ʽ��ʾ����
��ͼ����ABC�ǵȱ������Σ�P�ǡ�ABC��ƽ����BD��һ�㣬PE��AB�ڵ�E���߶�BP�Ĵ�ֱƽ���߽�BC�ڵ�F������Ϊ��Q�����BF=a����ôPE=$\frac{\sqrt{3}}{2}$a���ú�a�Ĵ���ʽ��ʾ����