题目内容
7.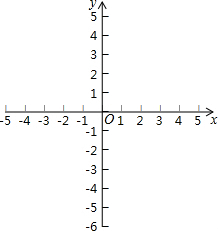 已知一次函数y=kx+b的图象与直线y=2x-$\sqrt{3}$平行,它与x轴、y轴分别相交于点A、B;它在y轴上的截距是4.平面直角坐标系的坐标原点为O.
已知一次函数y=kx+b的图象与直线y=2x-$\sqrt{3}$平行,它与x轴、y轴分别相交于点A、B;它在y轴上的截距是4.平面直角坐标系的坐标原点为O.(1)求这个一次函数的解析式,并在平面直角坐标系中画出函数的图象;
(2)在线段AB上求点P的坐标,使P、A、O三点成为等腰三角形的顶点;求点P的坐标.
分析 (1)根据已知条件“一次函数y=kx+b的图象与直线y=2x-$\sqrt{3}$平行”、“它在y轴上的截距是4”求得该一次函数解析式,由两点确定一条直线画出函数图象;
(2)需要对△PAO的底边进行分类讨论.根据两点间的距离公式和一次函数图象上点的坐标特征进行解答即可.
解答 解:(1)∵一次函数y=kx+b的图象与直线y=2x-$\sqrt{3}$平行,它与x轴、y轴分别相交于点A、B;它在y轴上的截距是4,
∴该一次函数解析式为:y=2x+4.
当x=0时,y=4.
当y=0时,x=-2.
则该直线经过点(0,4)和(-2,0),图象如图所示:
(2)如图,①当AP=OP时,点P在线段OA的中垂线上,此时x=-1,则y=2×(-1)+4=4.故P1(-1,2);
设P(x,2x+4).
②当OA=AP时,OA2=AP2,即4=(x+2)2+(2x+4)2,解得x=$\frac{10±2\sqrt{5}}{5}$,则y=$\frac{40±4\sqrt{5}}{5}$.
故P2($\frac{10+2\sqrt{5}}{5}$,$\frac{40+4\sqrt{5}}{5}$),P3($\frac{10-2\sqrt{5}}{5}$,$\frac{40-4\sqrt{5}}{5}$);
③当OA=OP时,OA2=OP2,即4=x2+(2x+4)2,解得x1=-1.2,x2=-2,
则y1=1.6,y2=0(舍去),
则P4(-1.2,1.6).
综上所述,符合条件的点P的坐标是:(-1,2)或($\frac{10+2\sqrt{5}}{5}$,$\frac{40+4\sqrt{5}}{5}$)或($\frac{10-2\sqrt{5}}{5}$,$\frac{40-4\sqrt{5}}{5}$)或(-1.2,1.6).
点评 本题考查了一次函数图象,等腰三角形的判定与性质,待定系数法求一次函数解析式等知识点.对于动点问题,应该进行分类讨论,以防漏解或错解.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案| A. | $\sqrt{2x+3}$+4=0 | B. | $\sqrt{x-7}$+$\sqrt{x}$=7 | C. | $\sqrt{x-3}$=1-x | D. | $\sqrt{x-1}$+$\sqrt{1-x}$=3 |
| A. | 钟表上的时针运动 | B. | 城市环路公共汽车 | ||
| C. | 地球绕太阳转动 | D. | 将等腰三角形沿着底边上的高对折 |
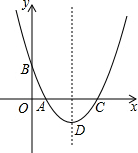 如图,已知二次函数y=x2+bx+c的图象关于直线x=2对称,且与x轴交于A、C两点,与y轴交于点B,点C与坐标原点不重合,其坐标为(c,0).
如图,已知二次函数y=x2+bx+c的图象关于直线x=2对称,且与x轴交于A、C两点,与y轴交于点B,点C与坐标原点不重合,其坐标为(c,0).