题目内容
18.已知点P(4,m),Q(n,-2)都在函数y=-$\frac{3}{2}$x的图象上,则m=-6,n=$\frac{4}{3}$.分析 把P、Q两点的坐标分别代入可得到关于m、n的方程,可求得m、n的值.
解答 解:
∵点P(4,m)在函数y=-$\frac{3}{2}$x的图象上,
∴m=-$\frac{3}{2}$×4=-6,
∵点Q(n,-2)在函数y=-$\frac{3}{2}$x的图象上,
∴-2=-$\frac{3}{2}$n,解得n=$\frac{4}{3}$,
故答案为:-6;$\frac{4}{3}$.
点评 本题主要考查一次函数图象上点的坐标特征,掌握函数图象上点的坐标满足函数解析式是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
13.已知$\frac{3}{x}$=$\frac{5}{y}$,则$\frac{{x}^{2}-xy+2{y}^{2}}{{x}^{2}-2xy}$的值为( )
| A. | -$\frac{44}{21}$ | B. | $\frac{8}{5}$ | C. | $\frac{44}{21}$ | D. | -$\frac{8}{5}$ |
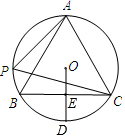 如图,A,P,B,C是⊙O上的四点,且满足∠BAC=∠APC=60°.
如图,A,P,B,C是⊙O上的四点,且满足∠BAC=∠APC=60°.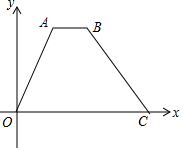 如图,在平面直角坐标系中,梯形ABCD的四个顶点的坐标分别是A(2,3$\sqrt{5}$),B(4,3$\sqrt{5}$),C(10,0),D(0,0).
如图,在平面直角坐标系中,梯形ABCD的四个顶点的坐标分别是A(2,3$\sqrt{5}$),B(4,3$\sqrt{5}$),C(10,0),D(0,0).